Random Points on a Sphere (Part 2)

Azimuth 2018-08-02

This is the tale of a mathematical adventure. Last time our hardy band of explorers discovered that if you randomly choose two points on the unit sphere in 1-, 2- or 4-dimensional space and look at the probability distribution of their distances, then the even moments of this probability distribution are always integers. I gave a proof using some group representation theory.

On the other hand, with the help of Mathematica, Greg Egan showed that we can work out these moments for a sphere in any dimension by actually doing the bloody integrals.

He looked at the nth moment of the distance for two randomly chosen points in the unit sphere in $\mathbb{R}^d,$ and he got

$\displaystyle{ \text{moment}(d,n) = \frac{2^{d+n-2} \Gamma(\frac{d}{2}) \Gamma(\frac{1}{2} (d+n-1))}{\sqrt{\pi} \, \Gamma(d+ \frac{n}{2} - 1)} }$

This looks pretty scary, but you can simplify it using the relation between the gamma function and factorials. Remember, for integers we have

$\Gamma(n) = (n-1)!$

We also need to know $\Gamma$ at half-integers, which we can get knowing

$\Gamma(\frac{1}{2}) = \sqrt{\pi}$

and

$\Gamma(x + 1) = x \Gamma(x)$

Using these we can express moment(d,n) in terms of factorials, but the details depend on whether d and n are even or odd.

I’m going to focus on the case where both the dimension d and the moment number n are even, so let

$d = 2e, \; n = 2m$

In this case we get

$\text{moment}(2e,2m) = \displaystyle{\frac{\binom{2(e+m-1)} {m}}{\binom{e+m-1}{m}} }$

Here ‘we’ means that Greg Egan did all the hard work:

From this formula

$\text{moment}(2e,2m) = \displaystyle{\frac{\binom{2(e+m-1)} {m}}{\binom{e+m-1}{m}} }$

you can show directly that the even moments in 4 dimensions are Catalan numbers:

$\text{moment}(4,2m) = C_{m+1}$

while in 2 dimensions they are binomial coefficients:

$\mathrm{moment}(2,2m) = \displaystyle{ {2m \choose m} }$

More precisely, they are ‘central’ binomial cofficients, forming the middle column of Pascal’s triangle:

$1, 2, 6, 20, 70, 252, 924, 3432, 12870, 48620, \dots$

So, it seems that with some real work one can get vastly more informative results than with my argument using group representation theory. The only thing you don’t get, so far, is an appealing explanation of why the even moments are integral in dimensions 1, 2 and 4.

The computational approach also opens up a huge new realm of questions! For example, are there any dimensions other than 1, 2 and 4 where the even moments are all integral?

I was especially curious about dimension 8, where the octonions live. Remember, 1, 2 and 4 are the dimensions of the associative normed division algebras, but there’s also a nonassociative normed division algebra in dimension 8: the octonions.

The d = 8 row seemed to have a fairly high fraction of integer entries:

I wondered if there were only finitely many entries in the 8th row that weren’t integers. Greg Egan did a calculation and replied:

The d=8 moments don’t seem to become all integers permanently at any point, but the non-integers become increasingly sparse.

He also got evidence suggesting that for any even dimension d, a large fraction of the even moments are integers. After some further conversation he found the nice way to think about this. Recall that

$\text{moment}(2e,2m) = \displaystyle{\frac{\binom{2(e+m-1)} {m}}{\binom{e+m-1}{m}} }$

If we let

$r = e-1$

then this moment is just

$\text{moment}(2r+2,2m) = \displaystyle{\frac{\binom{2(m+r)}{m}}{\binom{m+r}{m}} }$

so the question becomes: when is this an integer?

It’s good to think about this naively a bit. We can cancel out a bunch of stuff in that ratio of binomial coefficents and write it like this:

$\displaystyle{ \text{moment}(2r+2,2m) = \frac{(2r+m+1) \cdots (2r+2m)}{(r+1) \cdots (r+m)} }$

So when is this an integer? Let’s do the 8th moment in 4 dimensions:

$\text{moment}(4,8) = \displaystyle{ \frac{7 \cdot 8 \cdot 9 \cdot 10 }{2 \cdot 3 \cdot 4 \cdot 5} }$

This is an integer, namely the Catalan number 42: the Answer to the Ultimate Question of Life, the Universe, and Everything. But apparently we had to be a bit ‘lucky’ to get an integer. For example, we needed the 10 on top to deal with the 5 on the bottom.

It seems plausible that our chances of getting an integer increase as the moment gets big compared to the dimension. For example, try the 4th moment in dimension 10:

$\text{moment}(10,4) = \displaystyle{ \frac{11 \cdot 12}{5 \cdot 6}}$

This not an integer, because we’re just not multiplying enough numbers to handle the prime 5 in the denominator. The 6th moment in dimension 10 is also not an integer. But if we try the 8th moment, we get lucky:

$\text{moment}(10,8) = \displaystyle{ \frac{13 \cdot 14 \cdot 15 \cdot 16}{5 \cdot 6 \cdot 7 \cdot 8}}$

This is an integer! We’ve got enough in the numerator to handle everything in the denominator.

Greg posted a question about this on MathOverflow:

• Greg Egan, When does doubling the size of a set multiply the number of subsets by an integer?, 9 July 2018.

He got a very nice answer from a mysterious figure named Lucia, who pointed out relevant results from this interesting paper:

• Carl Pomerance, Divisors of the middle binomial coefficient, American Mathematical Monthly 122 (2015), 636–644.

Using these, Lucia proved a result that implies the following:

Theorem. If we fix a sphere of some even dimension, and look at the even moments of the probability distribution of distances between randomly chosen points on that sphere, from the 2nd moment to the (2m)th, the fraction of these that are integers approaches 1 as m → ∞.

On the other hand, Lucia also believes Pomerance’s techniques can be used to prove a result that would imply this:

Conjecture. If we fix a sphere of some even dimension > 4, and consider the even moments of the probability distribution of distances between randomly chosen points on that sphere, infinitely many of these are not integers.

In summary: we’re seeing a more or less typical rabbit-hole in mathematics. We started by trying to understand how noncommutative quaternions are on average. We figured that out, but we got sidetracked by thinking about how far points on a sphere are on average. We started calculating, we got interested in moments of the probability distribution of distances, we noticed that the Catalan numbers show up, and we got pulled into some representation theory and number theory!

I wouldn’t say our results are earth-shaking, but we definitely had fun and learned a thing or two. One thing at least is clear. In pure math, at least, it pays to follow the ideas wherever they lead. Math isn’t really divided into different branches—it’s all connected!

Afterword

Oh, and one more thing. Remember how this quest started with John D. Cook numerically computing the average of $|xy - yx|$ over unit quaternions? Well, he went on and numerically computed the average of $|(xy)z - x(yz)|$ over unit octonions!

• John D. Cook, How close is octonion multiplication to being associative?, 9 July 2018.

He showed the average is about 1.095, and he created this histogram:

Later, Greg Egan computed the exact value! It’s

$\displaystyle{ \frac{147456}{42875 \pi} \approx 1.0947335878 \dots }$

On Twitter, Christopher D. Long, whose handle is @octonion, pointed out the hidden beauty of this answer—it equals

$\displaystyle{ \frac{2^{14}3^2}{5^3 7^3 \pi} }$

Nice! Here’s how Greg did this calculation:

• Greg Egan, The average associator, 12 July 2018.

Details

If you want more details on the proof of this:

you should read Greg Egan’s question on Mathoverflow, Lucia’s reply, and Pomerance’s paper. Here is Greg’s question:

For natural numbers $m, r$ , consider the ratio of the number of subsets of size $m$ taken from a set of size $2(m+r)$ to the number of subsets of the same size taken from a set of size $m+r$ :

$\displaystyle{ R(m,r)=\frac{\binom{2(m+r)}{m}}{\binom{m+r}{m}} }$

For $r=0$ we have the central binomial coefficients, which of course are all integers:

$\displaystyle{ R(m,0)=\binom{2m}{m} }$

For $r=1$ we have the Catalan numbers, which again are integers:

$\displaystyle{ R(m,1)=\frac{\binom{2(m+1)}{m}}{m+1}=\frac{(2(m+1))!}{m!(m+2)!(m+1)}}$ $\displaystyle{ = \frac{(2(m+1))!}{(m+2)!(m+1)!}=C_{m+1}}$

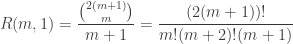
However, for any fixed $r\ge 2$ , while $R(m,r)$ seems to be mostly integral, it is not exclusively so. For example, with $m$ ranging from 0 to 20000, the number of times $R(m,r)$ is an integer for $r=$ 2,3,4,5 are 19583, 19485, 18566, and 18312 respectively.

I am seeking general criteria for $R(m,r)$ to be an integer.

Edited to add:

We can write:

$\displaystyle{ R(m,r) = \prod_{k=1}^m{\frac{m+2r+k}{r+k}} }$

So the denominator is the product of $m$ consecutive numbers $r+1, \ldots, m+r$ , while the numerator is the product of $m$ consecutive numbers $m+2r+1,\ldots,2m+2r$ . So there is a gap of $r$ between the last of the numbers in the denominator and the first of the numbers in the numerator.

Lucia replied:

Put $n=m+r$ , and then we can write $R(m,r)$ more conveniently as

$\displaystyle{ R(m,r) = \frac{(2n)!}{m! (n+r)!} \frac{m! r!}{n!} = \frac{\binom{2n}{n} }{\binom{n+r}{r}}. }$

So the question essentially becomes one about which numbers $n+k$ for $k=1, \ldots, r$ divide the middle binomial coefficient $\binom{2n}{n}$ . Obviously when $k=1$ , $n+1$ always divides the middle binomial coefficient, but what about other values of $k$ ? This is treated in a lovely Monthly article of Pomerance:

• Carl Pomerance, Divisors of the middle binomial coefficient, American Mathematical Monthly 122 (2015), 636–644.

Pomerance shows that for any $k \ge 2$ there are infinitely many integers with $n+k$ not dividing $\binom{2n}{n}$ , but the set of integers $n$ for which $n+k$ does divide $\binom{2n}{n}$ has density $1$ . So for any fixed $r$ , for a density $1$ set of values of $n$ one has that $(n+1), \ldots, (n+k)$ all divide $\binom{2n}{n}$ , which means that their lcm must divide $\binom{2n}{n}$ . But one can check without too much difficulty that the lcm of $n+1, \ldots, n+k$ is a multiple of $\binom{n+k}{k}$ , and so for fixed $r$ one deduces that $R(m,r)$ is an integer for a set of values $m$ with density 1. (Actually, Pomerance mentions explicitly in (5) of his paper that $(n+1)(n+2)\cdots (n+k)$ divides $\binom{2n}{n}$ for a set of full density.)

I haven’t quite shown that $R(m,r)$ is not an integer infinitely often for $r\ge 2$ , but I think this can be deduced from Pomerance’s paper (by modifying his Theorem 1).