The Big Internet Math-Off 2024, Round 1, Match 6

Here’s the sixth match in Round 1 of The Big Internet Math-Off. Today, we’re pitting Ayliean against K.P. Hart.

Take a look at both pitches, vote for the bit of maths that made you do the loudest “Aha!”, and if you know any more cool facts about either of the topics presented here, please write a comment below!

Ayliean – Maths Paths

Hello! Here is my pitch on the maths of paths (kinda), its a bit of a windy road!

But the real treasure was the maths we found on the way.

Here is a bonus fact for actually coming to The Aperiodical and checking out both pitches: All odd anti-prisms have eulerian paths so in theory can be made by balloon modelling a single balloon!

Bonus unlisted video:

Here is a link to the Demaine and Hart paper mentioned.

And I’ll take this opportunity to big up the maths community for always doing cool things like this, creating opportunities for each other, and taking an interest in each other’s work.

Ayliean (noun): Mathsy, arty, crochet crafty, origami, activist, zine author known for making badges and trouble. You can follow them on YouTube, as @Ayliean on all social media, or look at their homepage.

K.P. Hart – A rope around the Earth

One of the things I like about mathematics is that you can do mental experiments, things that would be impossible to do in real life.

Why would you do that? Well, it’s fun to think up ridiculous scenarios, “What if …”.

But occasionally such an experiment teaches you something unexpected, and you end up with some new insights.

Today’s experiment starts with a rope that fits snugly all around the Earth, say along the equator, or across the North and South Poles over the \(0\)- and \(180\)-degree meridians. So the length of the rope will be equal to the circumference of the Earth.

(Here we see the power of mathematics: we temporarily turn the earth into a perfect solid ball of rock, so that we have no problem doing the snug fitting. And we will keep our feet dry.)

Well, actually, our rope is a bit longer than the circumference and when we tie the ends together we end up with a closed rope around the earth that is exactly one metre longer than the circumference.

So, the rope is a bit of a loose fit now. The question is: How much looser?

Looseness 1

We could enlist a number of people to help us pull up the rope from the surface until it is a nice circle, concentric with the circle where we intended to fit the rope.

Our first way of measuring the looseness is the height we, and all the other people, have to pull up the rope in this way.

Ponder this for a while. If you already know the answer think of how you would explain this to a friend and what they may learn from this.

Looseness 2

We enlist nobody but we, at the North Pole, put the rope on a hook and pull it up until it is completely taut. (Imagine the Earth hanging suspended from that hook.)

Our second way of measuring the looseness is the height to which we have to raise the hook.

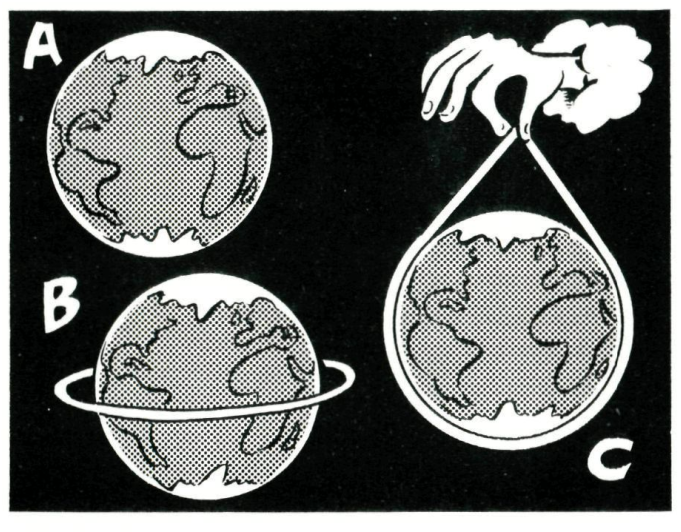Figure 1: The two questions in one picture.

Figure 1, from issue 1 of volume 24 of Pythagoras shows the what we are thinking about: in A the rope fits snugly around the Earth; in B the rope is lifted up everywhere to the same height; and in C we have a powerful being holding up the rope over the North Pole.

The answer to Looseness 1

Many people know the answer, but when I mention this question there often is someone who gives a wrong answer. The reason usually is that they are a bit too fast in their conclusion: “Earth is quite big, a metre is almost nothing, so, a millimetre maybe, or even less?”.

They would probably answer “No” to the question in the picture

Figure 2: Will a mouse be able to pass under it? From issue 2 of volume 44 of Pythagoras.

But if you pick a piece of paper and a pencil and write down what we are asking, the answer is easily found. We have the famous formula \(C=2\pi R\) for the circumference of a circle of radius \(R\). And we want to know how much \(R\) should increase so that \(C\) increases by \(1\). Well \[C+1 = 2\pi R +1 =2\pi R+\frac{2\pi}{2\pi}=2\pi\left(R+\frac1{2\pi}\right)\] We must increase \(R\) by \(1/(2\pi)\), which is about \(0.159\).

So our army of rope-raisers will have to lift the rope almost \(16\,\mathrm{cm}\). And the mouse will pass easily under the rope.

Insight

What did we learn? The important thing that we learned is that the initial size of \(C\), or \(R\), does not matter in this problem: to increase \(C\) by one metre, increase \(R\) by \(1/(2\pi)\) metre.

And how do we know this? Well, we never used the values of \(C\) and \(R\) in the calculation, only their relation.

The answer to Looseness 2

Figure 3 shows another picture from issue 2 of volume 44.

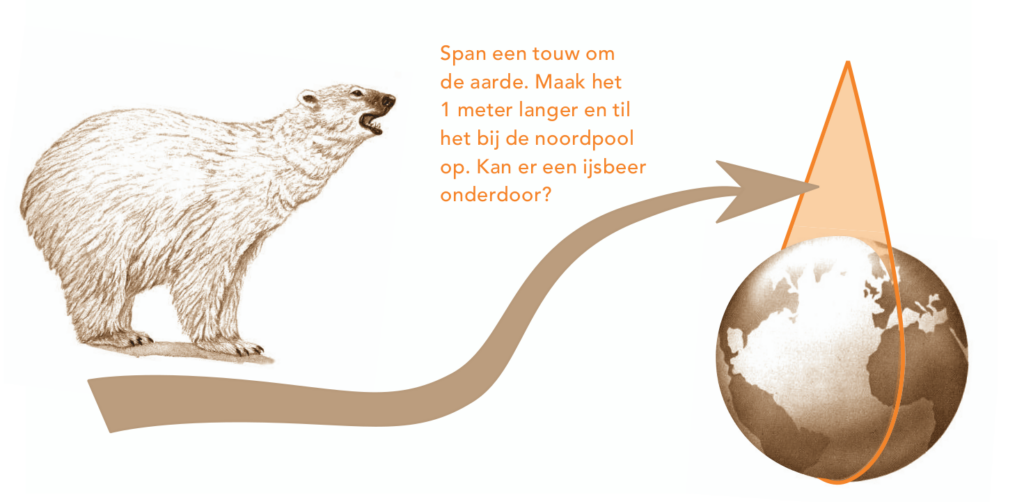Figure 3: Will a polar bear be able to pass under it?

It asks whether the second version of looseness will allow a polar bear to walk under the rope. Before you say “Yes” I should warn you that the picture is not to scale at all.

What I like about this particular problem is that you can answer it on a few different levels. Here I will give an answer that everybody with a decent calculator can verify.

In the video I will discuss further ramifications of this question and show how you might attack the problem with some first-year university Calculus under your belt.

First a picture

On of the first rules of mathematics is: draw a picture, if at all possible.

Figure 4: A sketch of the problem.

In Figure 4 we see the important part of the rope: the part above the surface of the Earth. Here is what the letters mean.

• \(h\) is the height of the hook, what we want to know.
• \(R\) is the radius of the Earth.
• \(A\) is where the rope detaches from the surface.
• \(d\) is the distance from \(A\) to the North Pole.
• \(\varepsilon\) is one half of the extra metre of rope.
• \(\alpha\) is the latitude, measured from the North Pole and in radians, of \(A\).

Now we stare at the picture for a while until we see some relations between the known quantities — \(R\) and \(\varepsilon\) — and the unknown quantities.

Since we work in radians we have \(d=\alpha\cdot R\). So \(d\) and \(\alpha\) are closely related.

Next: Pythagoras’ theorem (we have a right angle at \(A\)) tells us that \[(R+h)^2=R^2+(d+\varepsilon)^2\] which helps us to express \(h\) as a function of \(R\), \(\varepsilon\), and \(d\) (or \(\alpha\)) \[h=-R+\sqrt{R^2+(d+\varepsilon)^2}=-R+\sqrt{R^2+(\alpha R+\varepsilon)^2}\] So, all we need to do is calculate \(\alpha\) and we’re done.

We can find an equation for \(\alpha\) alone via another relation between \(\alpha\) and \(d\): \[\tan\alpha=\frac{d+\varepsilon}{R}\] if we put in \(\alpha=d/R\), then we get an equation just for \(\alpha\): \[\tan\alpha=\alpha+\frac\varepsilon{R}\] Well then, solve the equation for \(\alpha\), plug that value in the formula for \(h\) and Bob’s our uncle.

This is the sticky bit: the equation has no nice solution in closed form. And here is where a decent calculator comes in handy.

But first we need to put in the known values \(R\) and \(\varepsilon\). The latter is easy: \(\varepsilon=\frac12\) (in metres). For the former we use the original definition of the metre. It was chosen so that the meridian through Paris would measure exactly \(10\,000\,\mathrm{km}\) from the North Pole to the equator. This means that the circumference \(C\) is equal to \(40\,000\,000\,\mathrm{m}\), and hence that \(R=\frac{40000000}{2\pi}\,\mathrm{m}\). Putting that all together we see that we must solve \[\tan\alpha – \alpha = \frac\pi{40000000}\] Already in 2004 many calculators came with a solve button that would give you approximate solutions to equations; they would have no problem with this one.

You can also get a solution from Wolfram Alpha, you’ll get many and you need the one closest to \(0\).

I used the Maple program, it gave me \(\alpha=\mathtt{0.006176391781}\). If we plug that into \[h=-R+\sqrt{R^2+(\alpha R+\varepsilon)^2}\] we get \(h=\mathtt{121.430}\,\mathrm{m}\).

So there we have it: our polar bear will probably not even notice the rope as it is held quite high over the pole by our hook.

What’s in the video

In the video I will show how you can attack the problem using a bit of first-year university Calculus, most notably Taylor polynomials.

In the end we find an approximate formula for \(h\) in terms of \(R\) and \(\varepsilon\); that was the reason why I used \(\varepsilon\) and not just \(\frac12\) in the calculations: I was thinking ahead to this moment: \[h\approx \frac{\sqrt[3]9}2\cdot\varepsilon^{\frac23}\cdot R^{\frac 13}\] This formula explains why different values of \(R\) give noticeably different results.

Different values? Yes: the metre has changed length since its first definition, and in the time before calculators constants like \(R\) were found in tables, quite often rounded to the nearest kilometre, or nearest ten kilometres, or …. Better ways of measuring lead to changes too.

All that affects the outcome of our calculations, but not too much: all answers are roughly between \(121.4\,\mathrm{m}\) and \(121.5\,\mathrm{m}\).

K.P. Hart is a mathematician, general topologist, and occasional set theorist; he also writes for the Dutch math journal Pythagoras. You can follow him on Mathstodon, Bluesky, YouTube, or look at his homepage.

---

So, which bit of maths has tickled your fancy the most? Vote now!

Note: There is a poll embedded within this post, please visit the site to participate in this post's poll.

The poll closes at 08:00 BST tomorrow. Whoever wins the most votes will get the chance to tell us about more fun maths in the quarter-final.

Come back tomorrow for our seventh match in round 1, pitting Fran Herr against Tom Edgar, or check out the announcement post for your follow-along wall chart!