The Big Internet Math-Off 2024, Quarter-final 4

Here’s the last quarter-final match of The Big Internet Math-Off. Today, we’re pitting Ayliean against Dave Richeson.

Take a look at both pitches, vote for the bit of maths that made you do the loudest “Aha!”, and if you know any more cool facts about either of the topics presented here, please write a comment below!

Ayliean – Geometry and Oat Milk

One of the things I love about learning Maths is the extra layer of appreciation it adds to everything in the world around me.

Sometimes it will be the leaves of a plant, the movement of a crowd, the tiles on a pavement… this week, it was a weird shaped oat milk sachet.

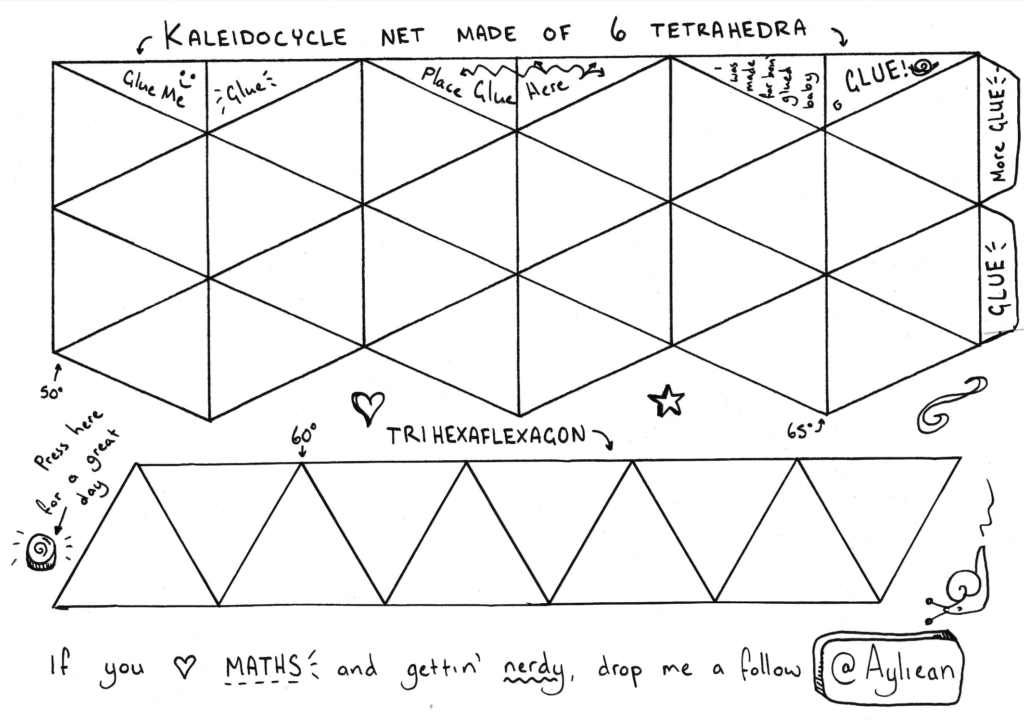
Here are some links of things for you to cut out and make yourself

A single printable page containing the net of a Flexahedron, and just enough space in the margin for a Tri-Hexa-Flexagon!

The stunning Möbius Flexahedron from OIST (it even comes in rainbow colour!)

The printable Truchet Tiles Zine, I wanna see these hiding in cafes for people to find and play with – get them printed, get them out there!

I hope you have as much fun cutting and folding these as I did – and please show me anything you make!

Stay nerdy,

Ayliean :)

Ayliean (noun): Mathsy, arty, crochet crafty, origami, activist, zine author known for making badges and trouble. You can follow them on YouTube, as @Ayliean on all social media, or look at their homepage.

Dave Richeson – A Doubly Surprising Calculator Trick

Who doesn’t love a calculator trick? It could be a simple one, like typing 0.7734, 376006, 57738461375, or some other carefully chosen number (yes, pre-teen boys, I know 5318008 is your favorite) into a calculator with a seven-segment display and turning it upside down to read HELLO, GOOGLE, or SLEIGHBELLS. It could also be more mathematical, such as having your friend perform a seemingly random sequence of steps that produces a pre-determined number. (Here’s one I just made up: type in any five-digit number, type it a second time [getting 2718227182, for instance], divide this by 11, divide this by your original five-digit number, subtract 1, divide by 9, and you will always get 1010.)

Being a mathematician, I was doubtful I could be surprised by a newcalculator trick, but when someone showed me this one, my mouth droppedopen.

To perform this simple trick, you will need a calculator that can do trigonometry.

Calculator trick

1. Set your calculator to degree mode.
2. Type several 5’s, such as 555555.
3. Press the \(1/x\) button.
4. Press the \(\sin\) button.

What do you notice? Cool, right?

Starting with 555555 and following these steps, the calculator on myphone spits out the value 0.000000031415958. After some 0’s are digitsthat look suspiciously like—but not exactly—the first digits of \(\pi\) (\(3.141592653589793\ldots\))!

Expressed another way, the calculator is telling me that \[10^8\cdot \sin(1/555555)=3.1415958\ldots,\] which agrees with \(\pi\) for the first six digits. Typing inmore 5’s is even better: the first 13 digits of \[10^{16}\cdot \sin(1/55555555555555)=3.141592653589825\ldots\] are correct. Surely, this isn’t acoincidence. What’s going on?

The interested and mathematically inclined reader may want to stopreading and see if they can give a justification. (But if you figure itout, come back since there’s a second trick that builds on this firstone.)

As a hint, this trick relies on the following three facts.

Fact 1. \(\frac{1}{180}=0.00\bar{5}\).

Fact 2. If \(\theta\) is measured in radians and \(\theta\) is approximately 0, then \(\sin\theta\approx \theta\).

Fact 3. Degrees and radians are related via theequation \[\theta_{\text{rad}}=\frac{\pi}{180}\cdot\theta_{\text{deg}}.\]

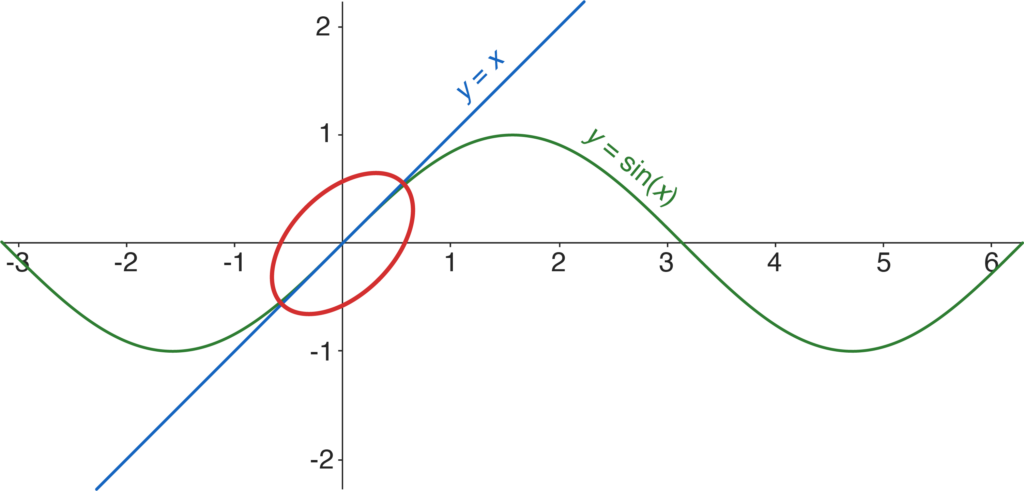
Fact 2 is illustrated in the figure below. In the circled region, thegraphs of \(y=x\) and \(y=\sin x\) are almostindistinguishable.

Let’s see why the trick works. Suppose we begin with a \(k\)-digit number of all 5’s: \(\overbrace{555\ldots 5}^k\). By Fact 1, \[\begin{aligned} \frac{1}{180}&=0.00\bar{5}\\ &\approx 0.00\overbrace{555\ldots 5}^k\\ &=(555\ldots 5)\cdot 10^{-k-2}. \end{aligned}\] Rearranging terms, this is equivalent to stating that \[\frac{1}{555\ldots 5}\approx 180\cdot 10^{-k-2}.\]

Fact 2 says that when \(\theta\) is given in radians and is approximately 0, \(\sin(\theta)\approx \theta.\) What if \(\theta\) is given in degrees? Let \(\sin_\text{rad}\) and \(\sin_\text{deg}\) be the radian-mode and the degree-mode sine functions, respectively. Then, using the degrees-to-radians conversion in Fact 3, \[\sin_\text{deg}(\theta)=\sin_\text{rad}\left(\frac{\pi}{180}\theta\right)\approx \frac{\pi}{180}\cdot \theta.\]

Putting this all together, we see that when our calculator is in degree mode, \[\begin{aligned} \sin\left(\frac{1}{555\ldots 5}\right)&\approx\frac{\pi}{180}\cdot\frac{1}{555\ldots 5}\\[0.5em]&\approx\frac{\pi} {180}(180\cdot 10^{-k-2})\\[0.5em]&=\pi\cdot 10^{-k-2}.\end{aligned}\]

So, \(10^{k+2}\cdot\sin\left(\frac{1}{555\ldots 5}\right)\approx\pi.\) That explains the trick!

[Performance note: This trick works for any number of 5’s in step 2.However, if the final value has many leading 0’s but not enough totrigger scientific notation, the “punchline” may be difficult torecognize. For instance, the input 5555555555555 yields0.000000000000003. For an iPhone calculator, I’d avoid using 10 to 13fives. If your friend does type that many, casually encourage them totype in a few more.]

The trick has one more surprise up its sleeve. We know that the digits following the string of 0’s is approximately \(\pi.\) How far off is it? What is \[10^{k+2}\cdot\sin\left(\frac{1}{555\ldots 5}\right)-\pi?\]

Here’s how to compute the error on your calculator.

Calculator trick (revisited) Calculate \(\sin\left(\frac{1}{555\ldots 5}\right)\) as in steps 1-4.

5. Press the \(\times\) button. 6. Type in “10”. 7. Press the \(x^y\) button. 8. If you had typed in \(k\) 5’s in step (2), type in the number \(k+2\). 9. Press “\(-\)”. 10. Press “\(\pi\)”. 11. Press “=”.

When I computed the error for my first example (with \(k=6\)), I got \(0.000003141595795.\) The number \(\pi\) appears again!

Wait. What? Why?

To understand why the error is related to \(\pi\), we must go back to the explanation of the first trick. We saw that \[\frac{1}{555\ldots 5}\approx 180\cdot 10^{-k-2},\] but in our analysis of the error, we need to be more exact and obtain an equality at this stage, not an approximation.

So we don’t have to wade through too much notation, let’s see the calculations for our six-digit number, 555555: \[\begin{aligned} \frac{1}{180}&=0.00\bar{5}\\ &=0.00555555\bar{5}\\ &=0.00555555+0.00000000\bar{5}\\ &=555555\cdot10^{-8}+10^{-6}\frac{1}{180}. \end{aligned}\] Moving these quantities around, we can rewrite that equality as \[\frac{1}{555555}=180\cdot \frac{10^{-8}}{1-10^{-6}}.\]

The exact same method applies if our initial number had \(k\) 5’s. We’d obtain the equality \[\frac{1}{555\ldots 5}=180\cdot\frac{10^{-k-2}}{1-10^{-k}}.\]

Because the calculator is in degree mode,

\[\begin{aligned} \sin\left(\frac{1}{555\ldots 5}\right)&\approx\frac{\pi}{180}\cdot \frac{1}{555\ldots 5}\\ &=\frac{\pi}{180}\left(180\cdot \frac{10^{-k-2}}{1-10^{-k}}\right)\\ &=\frac{\pi\cdot 10^{-k-2}}{1-10^{-k}}. \end{aligned}\] This implies that \[10^{k+2}\cdot \sin\left(\frac{1}{555\ldots 5}\right)\approx\frac{\pi}{1-10^{-k}}\approx \pi,\] as we concluded in the first trick. Here we are using the fact that when \(k\) is large (or even not too large) \(10^{-k}\approx 0,\) so \(\frac{1}{1-10^{-k}}\approx 1\).

But now, we can examine the error in this approximation: \[\begin{aligned} 10^{k+2}\sin\left(\frac{1}{555\ldots 5}\right)-\pi&\approx\frac{\pi}{1-10^{-k}}-\pi\\ &=\frac{\pi 10^k}{10^{k}-1}- \frac{\pi(10^{k}-1)}{10^{k}-1}\\ &=\pi\cdot \frac{1}{10^k-1}\\ &\approx \pi\cdot 10^{-k}, \end{aligned}\] as claimed!

Acknowledgments: I don’t know who discovered this trick. If you know, leave it in the comments! But the details of how I learned about it are found in my blog and in the comments (from almost 15 years ago!).

Dave Richeson is a professor of mathematics and the John J. & Ann Curley Faculty Chair in the Liberal Arts at Dickinson College in Carlisle, Pennsylvania, USA, and is the author of Euler’s Gem (Princeton University Press, 2008) and Tales of Impossibility (Princeton University Press, 2019). You can follow him on Mathstodon and X, or look at his homepage.

---

So, which bit of maths has tickled your fancy the most? Vote now!

Note: There is a poll embedded within this post, please visit the site to participate in this post's poll.

The poll closes at 08:00 BST tomorrow. Whoever wins the most votes will get the chance to tell us about more fun maths in the semi-final.

We’ve got a little break before the next round of the competition. Come back on the 17th for the first semi-final match, pitting Matt Enlow against Fran Herr, or check out the announcement post for your follow-along wall chart!