The Big Lock-Down Math-Off, Match 26

Welcome to the twenty-sixth and final match in this year’s Big Math-Off. Take a look at the two interesting bits of maths below, and vote for your favourite.

Here are today’s two pitches.

Colin Beveridge – The Miracle Sudoku

Colin blogs at flyingcoloursmaths.co.uk and tweets at @icecolbeveridge.

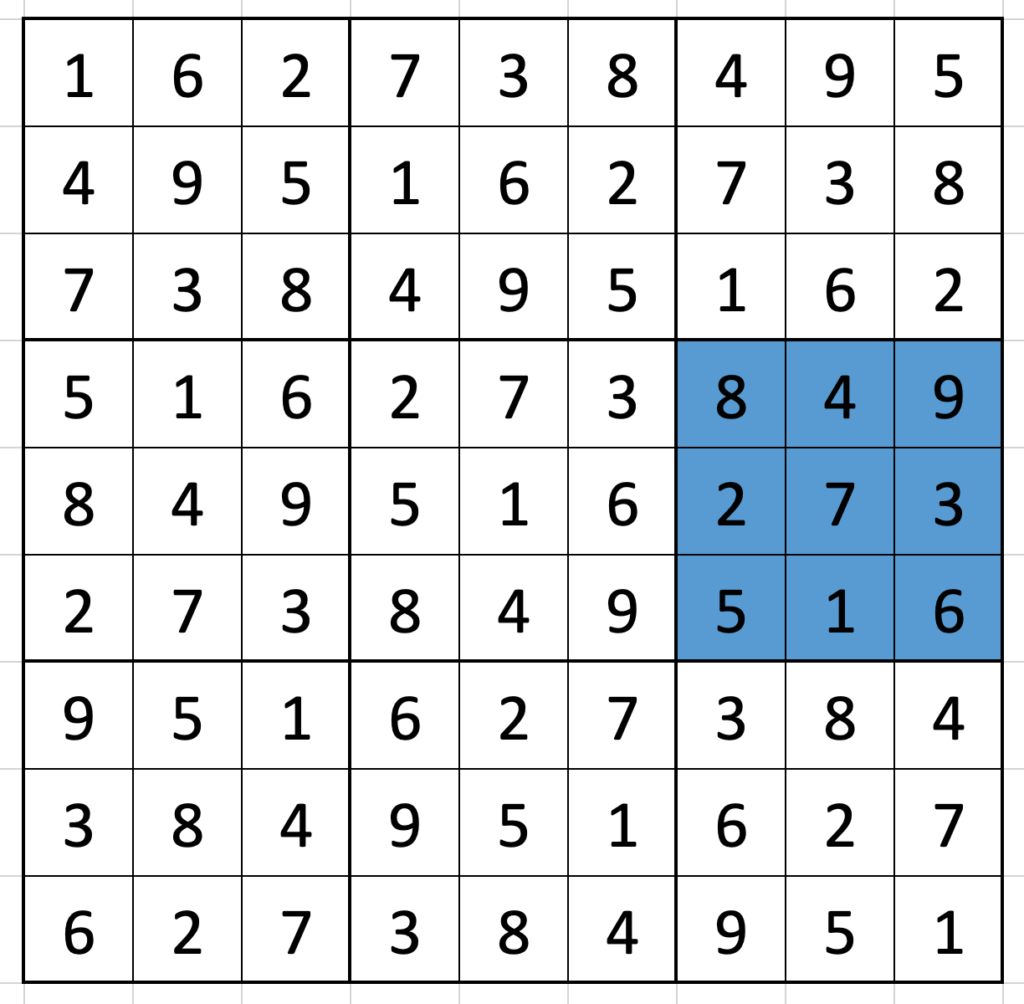
You’ve seen the Miracle Sudoku video, right? If not, watch the Miracle Sudoku video. I was skeptical, but it was absolutely worth 25 minutes of my time.

If you can’t be bothered to watch, the puzzle in question is a sudoku with three additional rules:

• No two cells separated by a chess king’s move may contain the same digit
• No two cells separated by a knight’s move may contain the same digit
• No two vertically/horizontally adjacent cells may contain consecutive digits.

(Try it yourself here!)

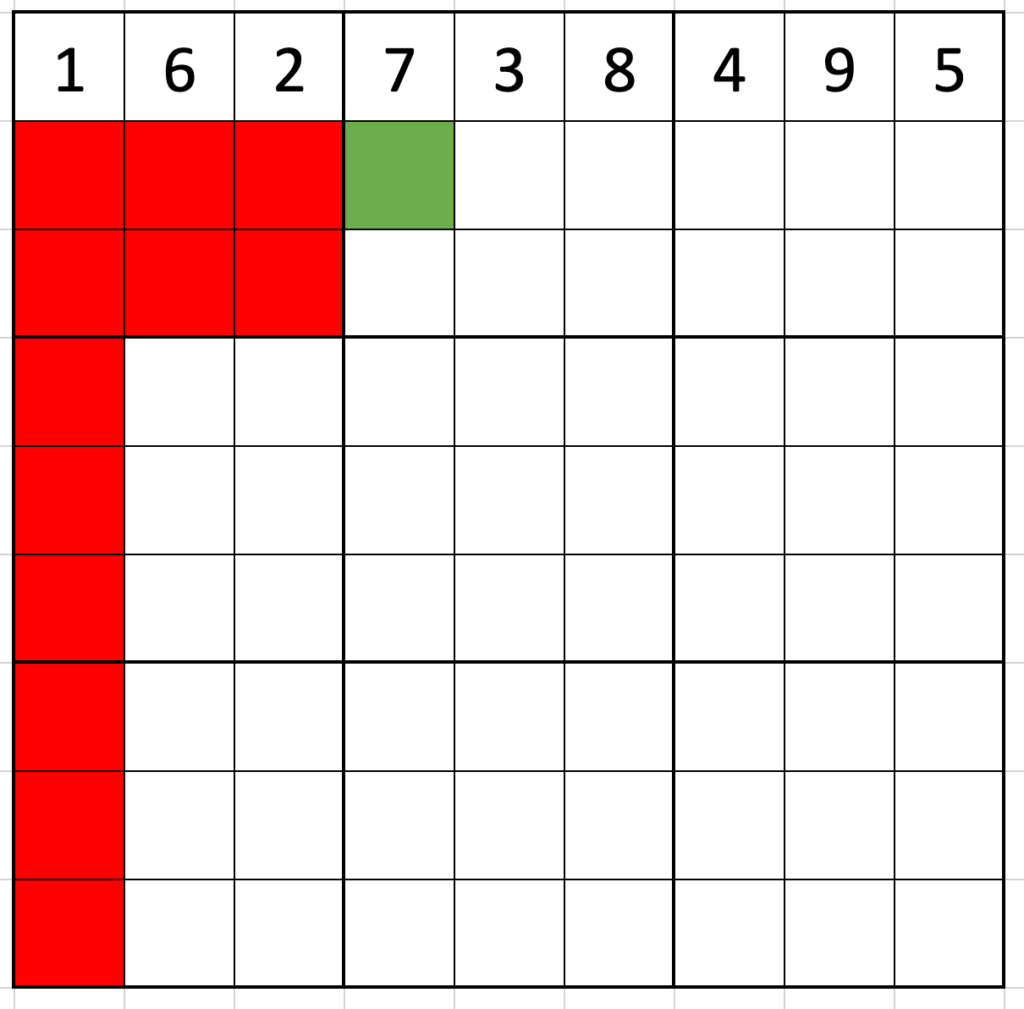
At the risk of minor spoilers, the solver in the video is skeptical that the puzzle presented can be solved; it has only two clues, and he suspects he is being trolled. Yet the puzzle can indeed be solved! Which, of course made me wonder: how many such puzzles are there?

As @realityminus3 has pointed out at least once, counting is hard, so I made a computer do it. It turns out, there are only 72 possible ‘miracle’ grids.

But wait, there’s more!

(Not more grids. More analysis.)

Is there some way of generating miracle grids? . When I looked closely at the 72 possibilities, some things looked… awfully familiar. Repetitive, even.

For example, every sudoku (not just the miracle flavour) has one column that starts with a 9 and one column that ends in a 9; the same is true for rows – and for any digit: I just happened to pick 9. Let’s call those the 9-strings.

In all of the miracle grids, the four 9-strings (in some order) are

• 936|471|825,
• 948|372|615,
• 951|627|384 and
• 963|528|174

… and the middle two of those cracked it open!

How? Look at the alternate digits: in the second one, you’ll see 9-8|-7-|6-5 and -4-|3-2|-1-; in the third, it’s 9-1|-2-|3-4 and -5-|6-7|-8-: you just count up or down, skipping a space each time.

• 
• 

Looking more closely at each grid, either the rows or the columns do the skip-counting, and all in the same direction. This is how we build it!

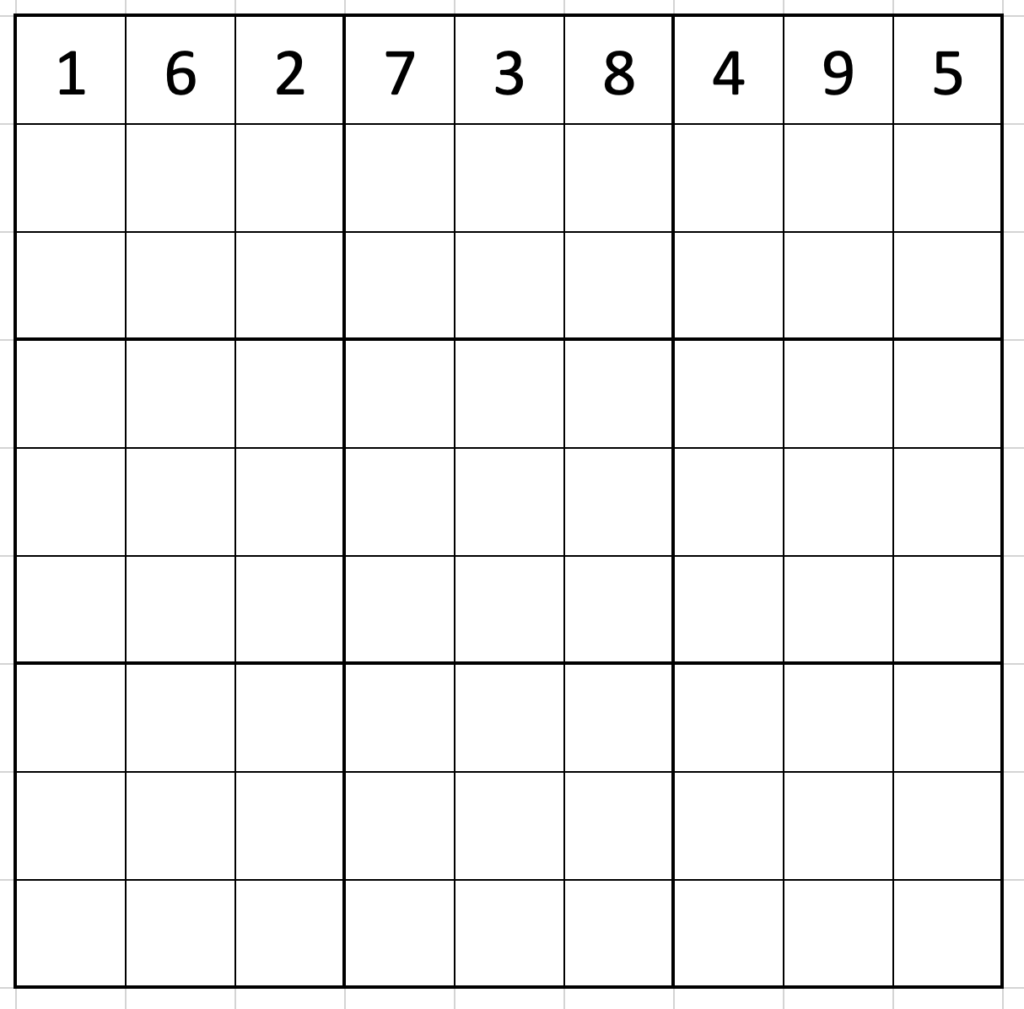
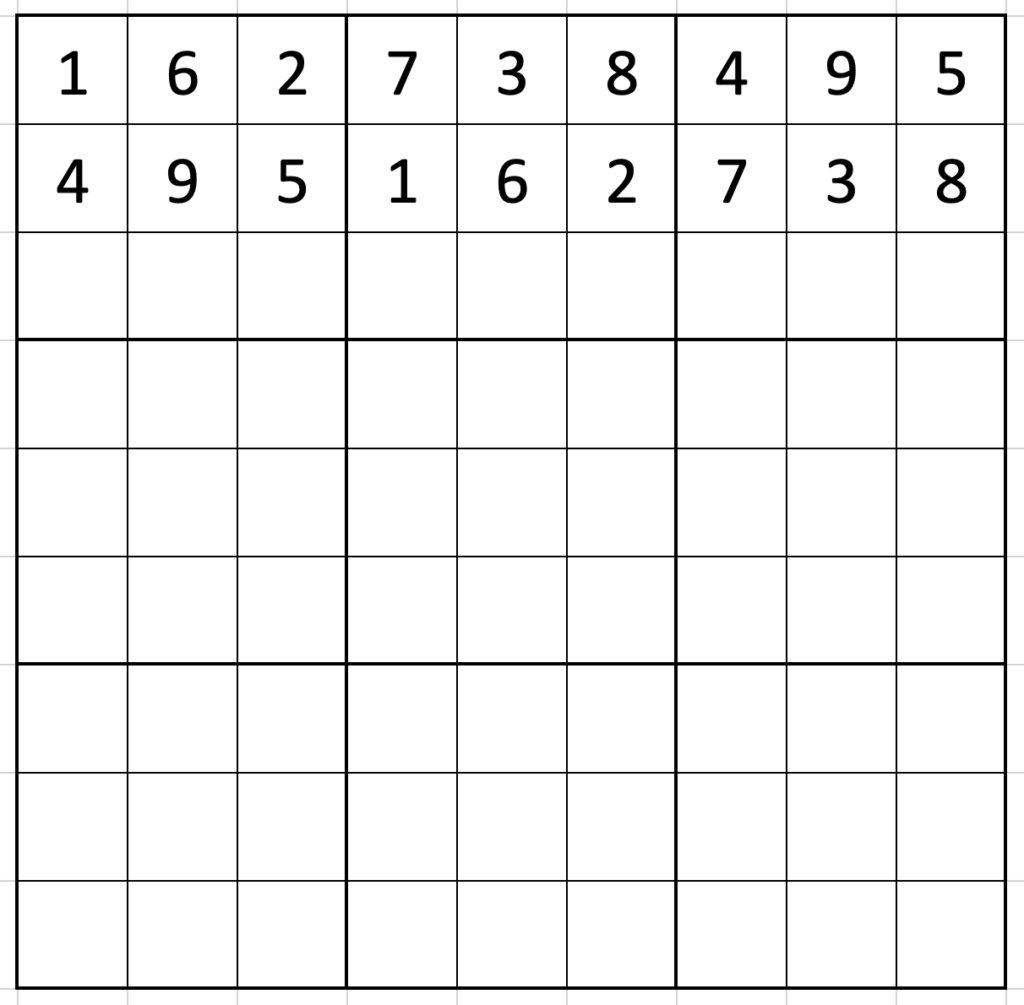
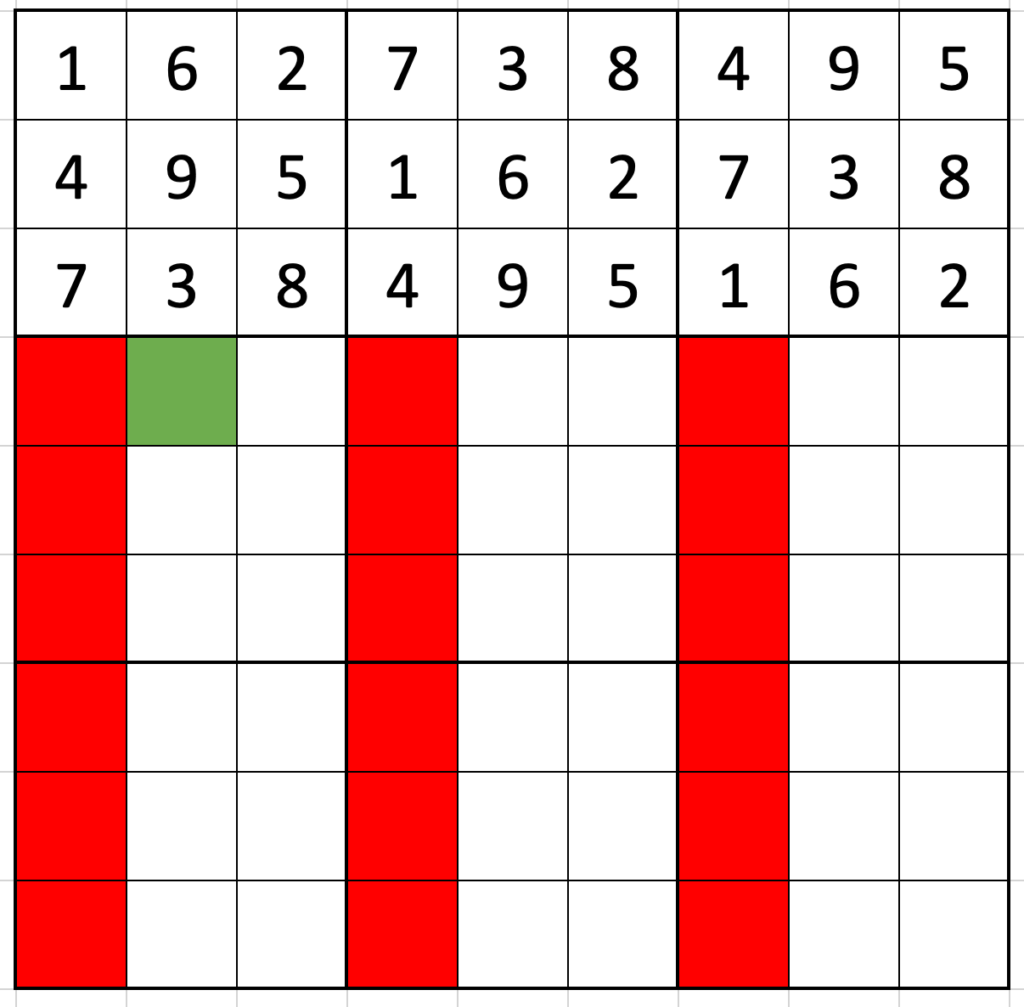
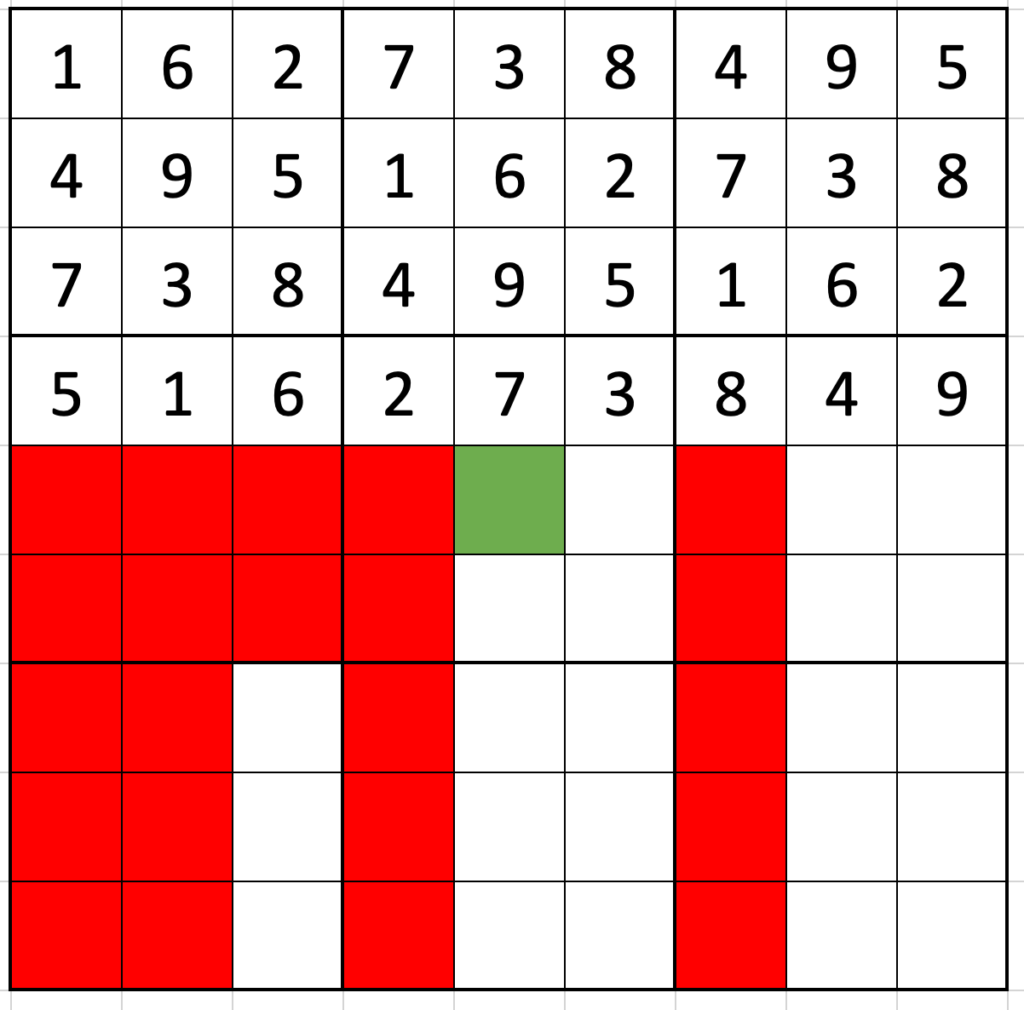
Pick a digit to go in the top-left corner. (Say 1. It doesn’t really matter.) Using the skip-counting, fill in the top row as 162|738|495.

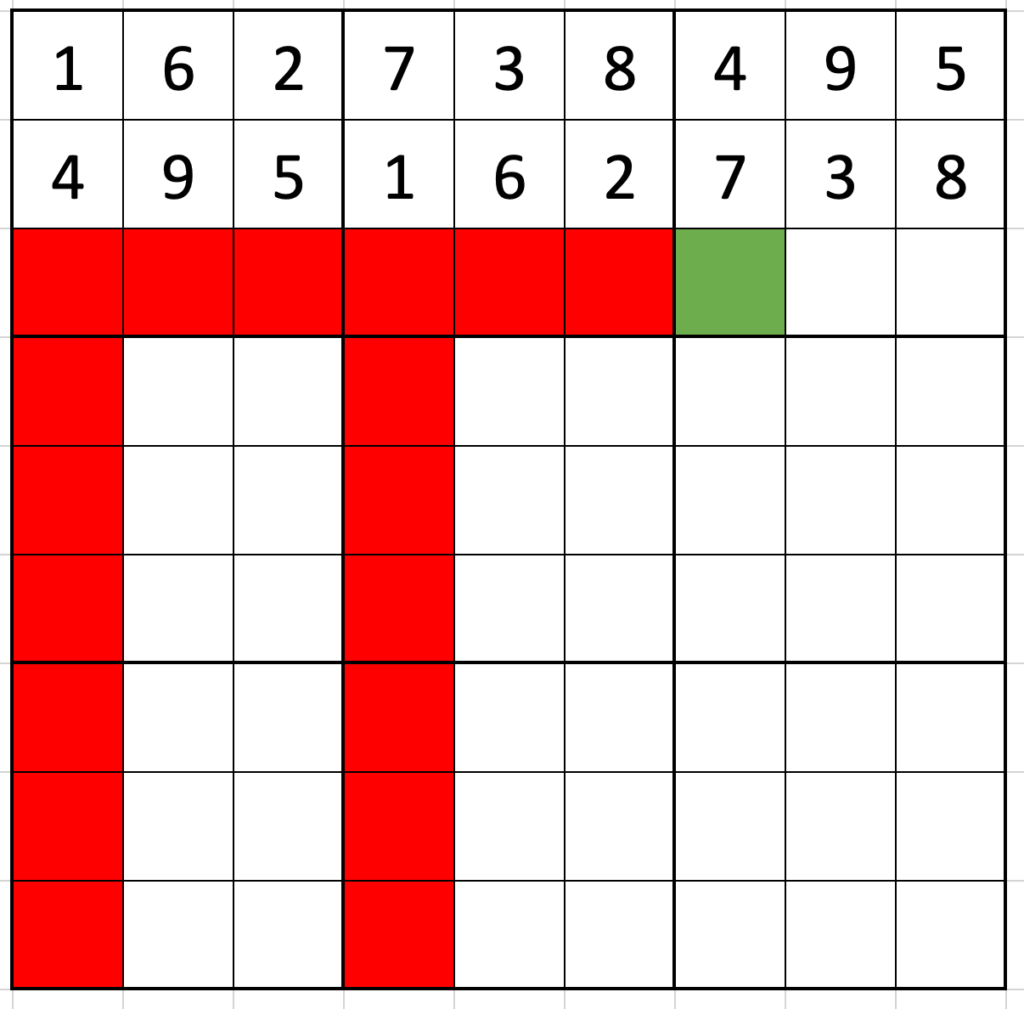
Now, where’s the first place the 1 can go in the second row? It can’t go in the first three spaces because there would be two 1s in the first box, so the first place it can go is in the fourth column. Putting the 1 there means filling out the second row as 495|162|738 (the first row moved on by three spaces).

• 
• 

Similarly, the first place the 1 of the third row can go is in column seven, and the third row is again a simple twist of the first: 738|495|162.

• 
• 

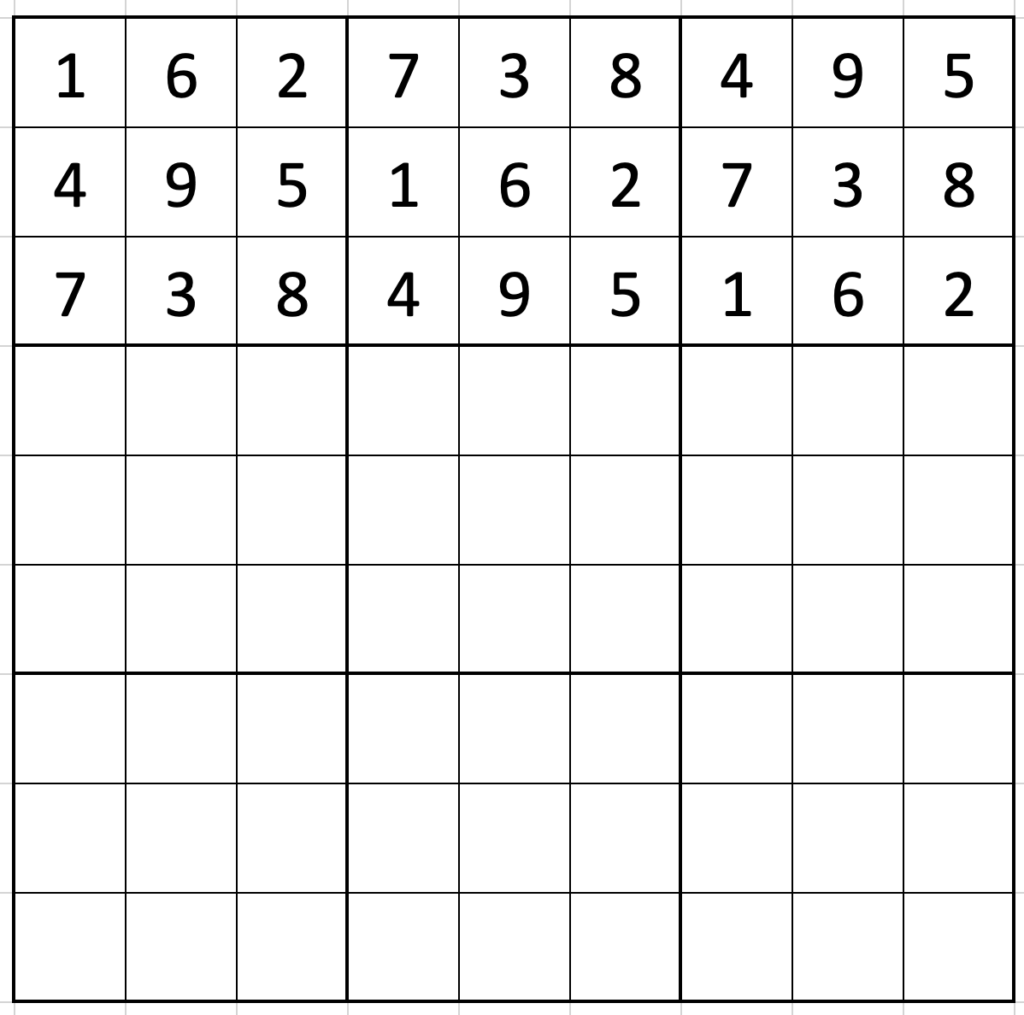
The same logic continues down the grid: the first place a 1 can go in row four is column 2 (516|273|849), and the first place in row 5 is position 5 (849|516|273).

• 
• 
• 

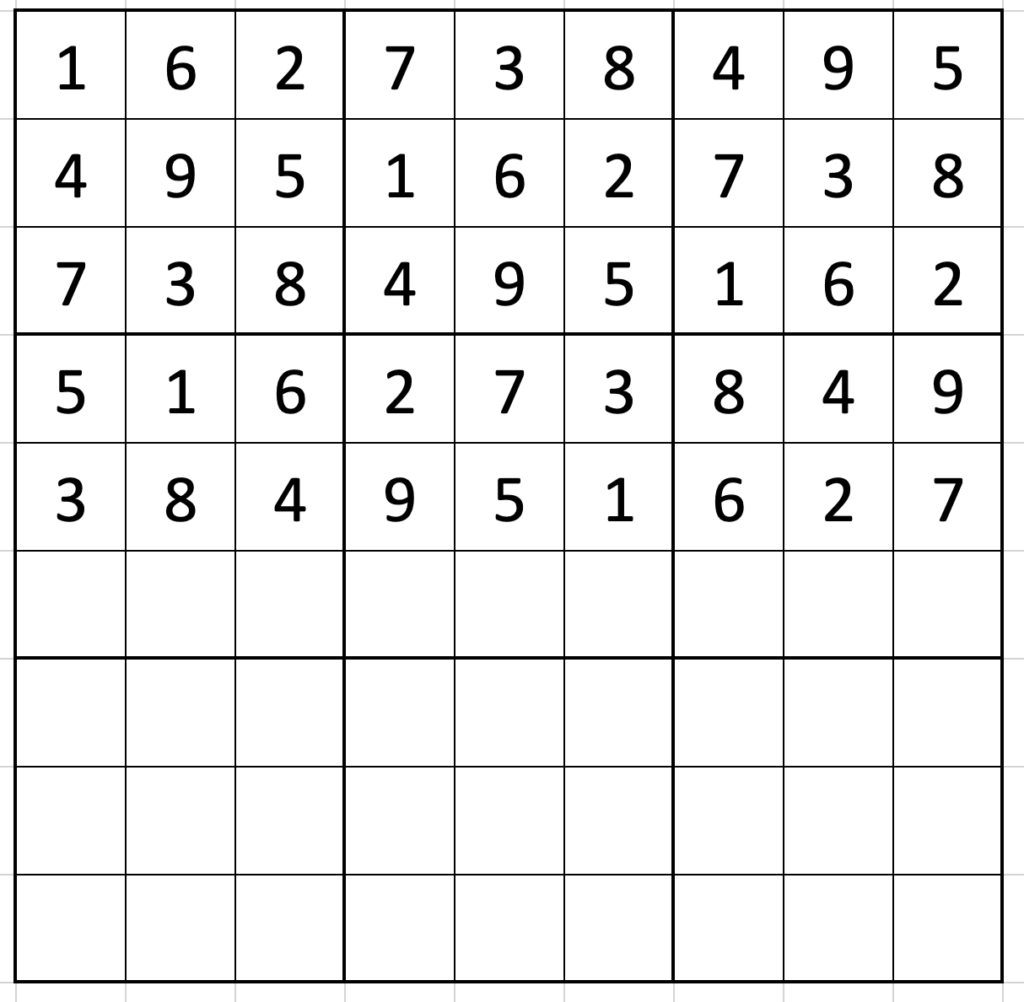
You can probably complete the grid by yourself from there:

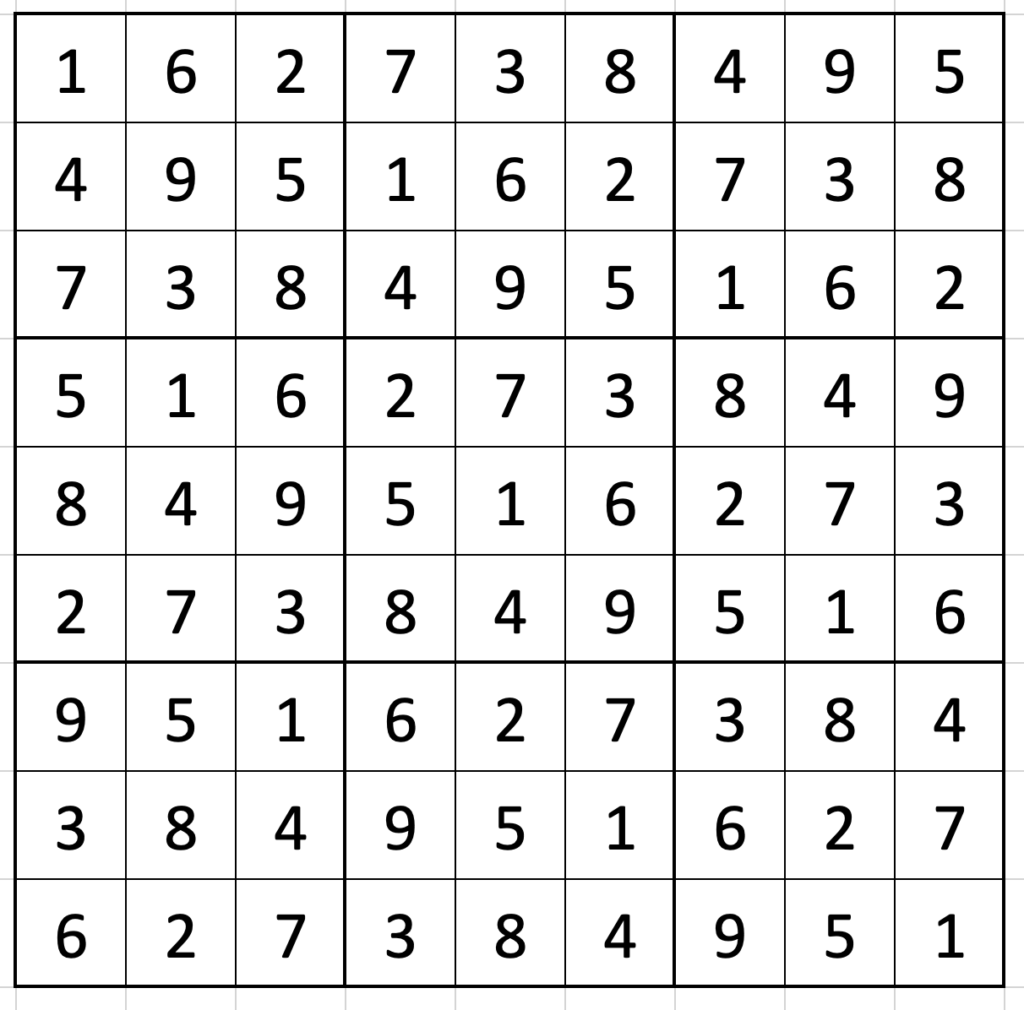
There are eight ways to reflect and/or rotate the grid (the 1 you started with could go in any of the four corners, and the 162 could go vertically or horizontally), and nine digits you could start from in the top left – accounting for all 72 possible grids!

Easter Eggs and Open Questions

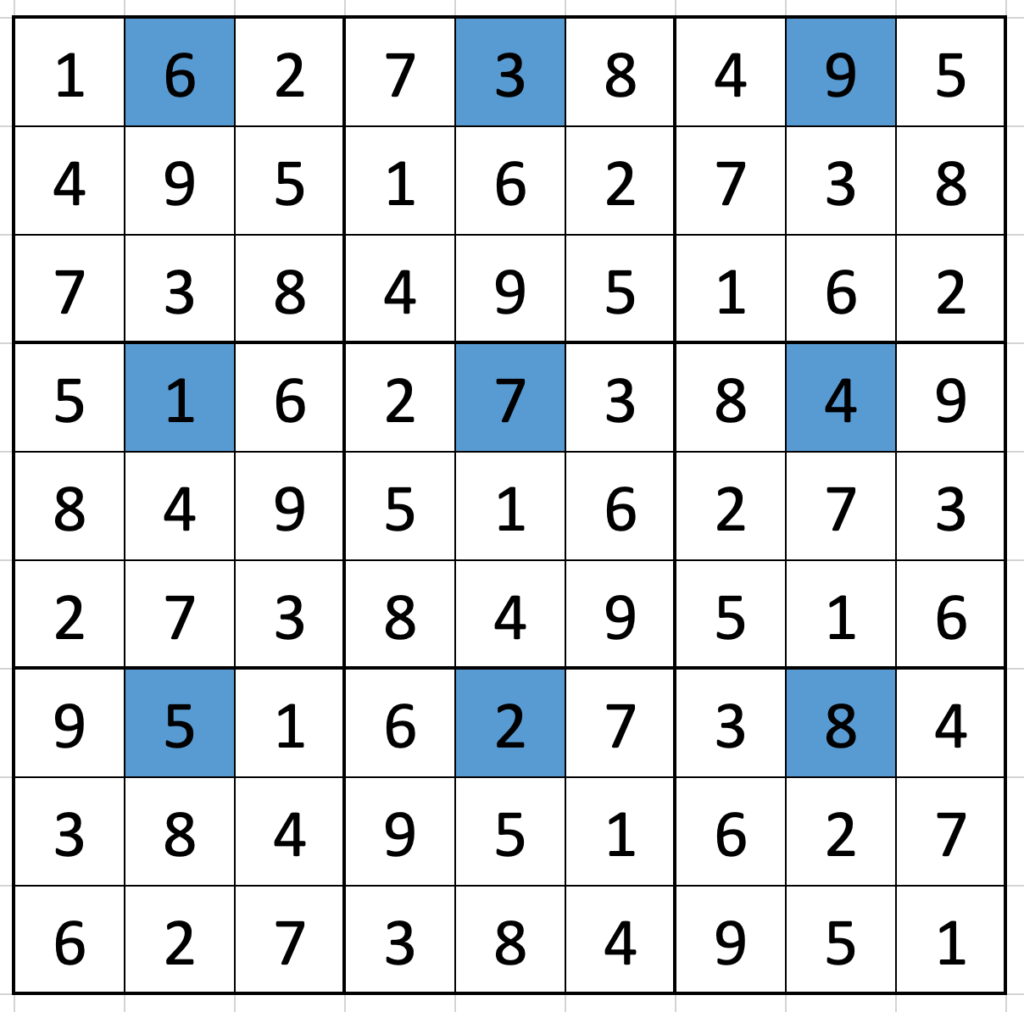
• Pick a position in a 3-by-3 box – say the top middle. Write out the digits in that position for each box to form a 3-by-3-square. This box, when reflected across the minor diagonal, is in the grid. It’s in the position reflected across the minor diagonal from the position you picked (top-middle reflects to middle-right):

• 
• 

• In any row of 3-by-3 boxes, look at the diagonals moving up and to the right, wrapping around the top of the box and either end of the row. The offset is 1 each time.

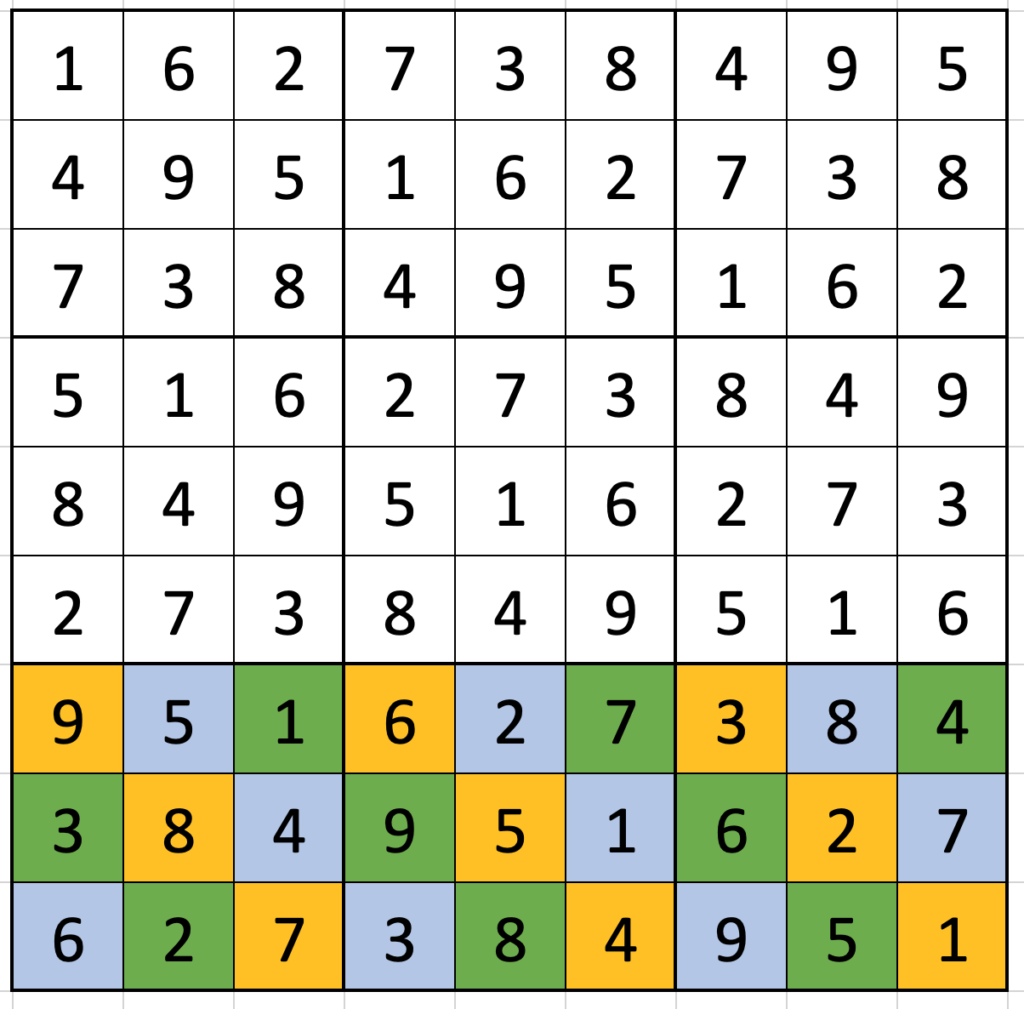
• The box with a 5 as its middle number? That’s a magic square. In fact, any digit 5 is at the centre of a magic square if you wrap the same way as in the previous bullet.

Some questions that are open (at least for me):

• Under what circumstances do two digits uniquely determine the whole grid? (My code says there are 87408 = 72×2×607 clue pairs that give unique solutions.)
• Under which of those circumstances would @crypticcracking be able to solve it?

CreativeCrocheter – Three Geometries in Crochet

CreativeCrocheter is the pseudonym of a person who blogs about crochet and maths.

As part of a math symposium at my undergraduate alma mater, I set up “learning stations” with my crocheted items that demonstrated various mathematical concepts. You’ve already seen the first station’s challenge if you voted in Match 5.    The second station contained three crocheted objects – yes, the school team colors are purple and gold.

I invited the attendees (who included a number of local weavers!) to consider the following:

1. There are 3 objects, that will be referred to as follows:
   1. Object A is the solid purple object
   2. Object B is the purple and gold object
   3. Object C is the purple and white object
2. These objects share the following characteristics:
   1. All three were crocheted with the same hook and the same diameter yarns
   2. All three started with the same number of stitches in the first round
   3. All three were worked in continuous spirals of stitches
   4. All three have 16 rounds of stitching
3. Name the type of geometry exemplified by each object
4. Hypothesize how to determine the curvature of each object
5. What other items in nature share the characteristics of Object B?
6. What type of spiral appears on Object C? Alternatively, what search terms would you enter in an an Internet search engine to find the name of the spiral?

Bonus for fiber folk: Why did the purple and white object take on a hexagonal shape?

Once everyone had a chance to look and consider, we discussed their answers and also considered the following:

1. How might you use objects such as these to engage non-mathematicians in exploring various geometries?
2. What would you do to demonstrate the parallel axiom in each geometry using these objects? This would be a good student topic for a future talk.

Ready for some answers?

• Object A: Euclidean plane – the two colors form an Archimedean spiral, where each spiral arm remains the same width, created by increasing the number of stitches in each round by the same number as we started with.
• Object B: hyperbolic plane (also called saddle or Lobachevskian geometry) – its geometry is shared by lettuce leaves, the saddleback on a mountain, and the crotch of your slacks, to name just a few, and is created by increasing in each round by more stitches than we started with.
• Object C: ideal sphere (spherical geometry, also called elliptic or Riemannian) – there are fewer increases in each round for the first half, then corresponding numbers of decreases in the second half to close the sphere.

For more, do explore some of the sources and inspirations for this exercise!

• Susan Lombardo
• Woolly Thoughts
• Daina Taimiņa
• Margaret Wertheim
• Ms Premise-Conclusion (ideal sphere pattern and other geekery)
• Bridges

Oh, that bonus question? A crocheted spiral forms a regular polygon when the increases (two stitches placed into the same stitch) align – in this case by always increasing in the second stitch of the increase done in the previous round. The resulting polygon has the same number of sides as the number of increases per round. So starting with 6 stitches, as I did for each of these shapes, gives a hexagon.

As noted in some previous matches, the supposed dichotomy between logical thinkers and creative thinkers simply doesn’t hold up when it comes to exploring math concepts with fiber!

---

So, which bit of maths made you say “Aha!” the loudest? Vote:

Note: There is a poll embedded within this post, please visit the site to participate in this post's poll.

The poll closes at 9am BST on Wednesday the 3rd. I think this is the last match of this year’s math-off. Thanks for reading, and thanks for playing!