Given a smooth compact Riemannian manifold  , the incompressible Euler equations can be written in abstract index notation as
, the incompressible Euler equations can be written in abstract index notation as
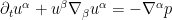
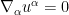
where

is a time-dependent scalar field (representing pressure), and
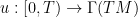
is a time-dependent vector field (representing fluid velocity). Here
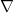
is the
Levi-Civita connection associated to
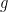
. One can recover
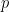
from

(up to constants), so I will abuse notation and refer to the solution to this system as

rather than
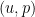
. Over the last few years I have been interested in the following conjecture:
Conjecture 1 (Finite time blowup) There exists a manifold 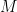 and a smooth solution
and a smooth solution  to the Euler equations that blows up at some finite time
to the Euler equations that blows up at some finite time  .
.
This remains open, however there has been progress on rougher versions of this problem. For instance, there is the well-known result of Elgindi (discussed in this previous post) that when  and
and 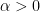 is sufficiently small, there exists a
is sufficiently small, there exists a  solution
solution  to the Euler equations on
to the Euler equations on 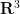 that blows up in finite time. There has also been progress in establishing various “universality” properties of the Euler flow on manifolds (which informally state that “fluid computers” are possible); see for instance this recent survey of Cardona, Miranda, and Peralta-Salas. Unfortunately, these “fluid computers” do not combine well with scaling symmetries, and so thus far have not been able to produce (finite energy) blowups.
that blows up in finite time. There has also been progress in establishing various “universality” properties of the Euler flow on manifolds (which informally state that “fluid computers” are possible); see for instance this recent survey of Cardona, Miranda, and Peralta-Salas. Unfortunately, these “fluid computers” do not combine well with scaling symmetries, and so thus far have not been able to produce (finite energy) blowups.
I have been playing with one approach to this conjecture, which reduces to solving a certain underdetermined system of partial differential equations, and then establishing some stability result for the resulting solution. However, I have not been able to make headway on solving this latter system despite its underdetermined nature; so I thought I would record my partial attempt here in case anyone is interested in pursuing it further (and also to contribute to the practice of sharing unsuccessful attempts to solve a problem, which is still quite infrequently done in our community).
To avoid technicalities let us simplify the problem by adding a forcing term  :
:
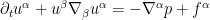
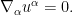
Standard local well-posedness theory (using the vorticity-stream formulation of the Euler equations) tells us that this problem is well-posed if the initial data
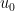
is divergence free and in
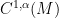
for some
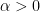
, and the forcing term

is in
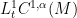
. We have the following
recent result of Córdoba and Martínez-Zoroa, solving a version of the above conjecture in the presence of a reasonably regular forcing term:
Theorem 2 (Finite time blowup for the forced equation) There exists a smooth solution to the forced Euler equations on 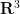 that exhibits finite time blowup, in which the forcing term
that exhibits finite time blowup, in which the forcing term  stays uniformly bounded in
stays uniformly bounded in  for any
for any  .
.
Roughly speaking, their argument proceeds by a multiscale construction, in which the solution is set up to eventually have some presence at a spatial scale  , which is conducive to generating an exponential “stretching” of a small forcing term at a much higher spatial scale
, which is conducive to generating an exponential “stretching” of a small forcing term at a much higher spatial scale 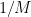 , which one then introduces to then set up the solution for the next scale.
, which one then introduces to then set up the solution for the next scale.
As a model problem, I tried to reproduce this type of result from a more geometric perspective, trying to aim for a more “self-similar” blowup than a “multi-scale” one, in the hope that this latter type of blowup might be more tractable to analyze and eventually resolve Conjecture 1. I didn’t fully succeed; but I think the approach I outline below is in principle feasible.
The manifold I will work on is a cylinder  , where
, where  is a smooth compact manifold, and the metric on
is a smooth compact manifold, and the metric on 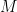 is just the sum of the standard metric
is just the sum of the standard metric  on the first coordinate and
on the first coordinate and 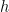 :
:
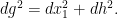
(I have experimented with working with more warped metrics to gain more flexibility, but this seems to only influence lower order terms. However, such tricks may be useful to improve the regularity of the forcing term, or perhaps even to eliminate it entirely.) The idea is to try to create a solution that blows up on a slice
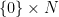
on this cylinder, but stays smooth until the blowup time, and also uniformly smooth away from this slice. As such, one can localize the solution away from this slice, and replace the unbounded component
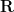
of
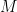
by a compact circle
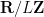
for some large
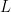
if desired. However, I prefer to work with the unbounded component
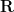
here in order to scale in this direction.
If we now use Greek indices to only denote coordinates in the “vertical” coordinate  , the velocity field
, the velocity field  now becomes
now becomes  , and the Euler equations now split as
, and the Euler equations now split as
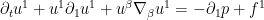
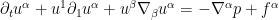
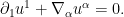
If the solution is concentrating in a narrow neighborhood of the slice
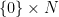
, we expect the terms involving
to be quite large, and the terms involving
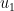
to be rather small. This suggests that the
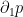
pressure term is going to be more significant than the
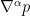
term. We therefore select the forcing term to cancel this term by choosing
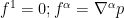
leaving us with the simplified equation
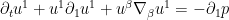
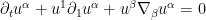
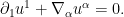
The nice thing about this latter equation is that the first equation is basically just a formula for
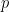
and so can be dropped, leaving us with
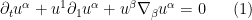

This equation now admits a two-parameter family of scale invariances
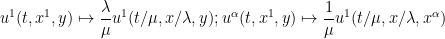
for
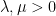
, where we use
to ednote the

coordinate. It also inherits an energy conservation law from the original Euler equations; the conserved energy is

using the metric on

to raise and lower the Greek indices.
It is now tempting to try to set up an approximately scale-invariant blowup solution. It seems that the first step in this is to construct a “soliton” type localized steady state solution, that is a solution  ,
,  to the equation
to the equation
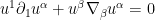
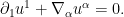
that decays in the
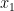
variable; one can then hope to do a suitable stability (or instability) analysis of this soliton to perturb it to a blowup solution, as there are many results of this type for other equations that one could use as a model. The energy conservation law does constrain to some extent the nature of the blowup (basically, the two scaling parameters
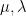
above become linked by the relation
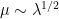
), but does not seem to otherwise prevent such a blowup from occuring.
Analytically, this is not a particularly pleasant equation to try to solve; one can substitute the second equation into the first to obtain a single equation
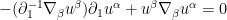
but the inverse derivative
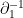
is difficult to work with and seems to create ill-posedness (somewhat reminiscent of the ill-posedness of the Prandtl
boundary layer equation).
Nevertheless, one can still attempt to solve this equation by separation of variables. If one makes the ansatz
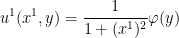
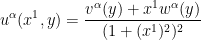
for some smooth
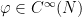
and
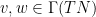
, some calculation shows that the system now reduces to a system purely on

:
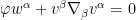
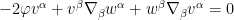
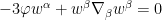
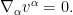
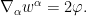
The metric 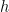 is hidden in this system through the covariant derivative
is hidden in this system through the covariant derivative 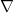 . To eliminate the metric, we can lower indices to write
. To eliminate the metric, we can lower indices to write

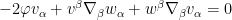
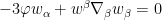
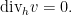
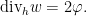
Here the divergence is relative to the volume form induced by
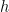
, but by a dimension lifting trick (see Section 3 of
this paper of mine) one can replace this divergence with a divergence
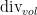
with respect to any other volume form on

. We have the identity
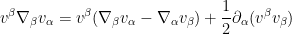
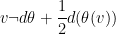
where we have switched to coordinate-free notation, and
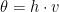
is the

-form associated to

. If we similarly let
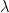
be the

-form associated to
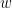
, and eliminate
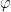
, the system now becomes



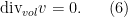
Also, the fact that

are dual to
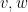
with respect to some unspecified Riemannian metric
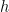
turns out to essentially be equivalent to the assumption that the Gram matrix is positive definite,
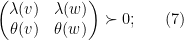
see Section 4 of
the aforementioned paper. This looks like a rather strange system; but it is three vector equations
(3),
(4),
(5) in four vector (or one-form) unknowns
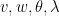
, together with a divergence-free condition
(6) and a positive definiteness condition
(7), which I view as basically being scalar conditions. Thus, this system becomes underdetermined when the dimension of

is large enough (in fact a naive count of degrees of freedom suggests that dimension at least three should be sufficient). It should thus be possible to locate an abundant number of solutions to this system; but to my frustration, the system is just barely complicated enough to prevent me from simplifying it to the point where it becomes evident how to construct solutions; in particular, I have not been able to find a viable further ansatz to transform the system to a more tractable one. Part of the problem is that while the system is technically underdetermined, there are not that many degrees of freedom to spare to ensure this underdetermined nature, so one cannot afford to make an ansatz that sacrifices too many of these degrees of freedom. In my previous paper I was able to use a very symmetric construction (taking

to basically be the product of an orthogonal group and a torus) to solve a similar system that was in fact quite overdetermined, but I have not been able to exploit such symmetries here. I have also experimented with other separation of variable ansatzes, but they tend to give similar systems to the ones here (up to some changes in the coefficients).
Remark 3 One can also try to directy create a self-similar blowup to (1), (2), for instance by making the ansatz 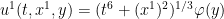
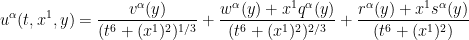
for 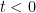 and some fields
and some fields  and
and  . This particular ansatz seems consistent with all known conservation laws; however it works out to basically be ten vector equations (plus some additional scalar constraints) on ten vector field unknowns, so is just barely overdetermined. I have not been able to locate a self-similar blowup ansatz that is underdetermined.
. This particular ansatz seems consistent with all known conservation laws; however it works out to basically be ten vector equations (plus some additional scalar constraints) on ten vector field unknowns, so is just barely overdetermined. I have not been able to locate a self-similar blowup ansatz that is underdetermined.
, the incompressible Euler equations can be written in abstract index notation as
and a smooth solution
to the Euler equations that blows up at some finite time
.
and
is sufficiently small, there exists a
solution
to the Euler equations on
that blows up in finite time. There has also been progress in establishing various “universality” properties of the Euler flow on manifolds (which informally state that “fluid computers” are possible); see for instance this recent survey of Cardona, Miranda, and Peralta-Salas. Unfortunately, these “fluid computers” do not combine well with scaling symmetries, and so thus far have not been able to produce (finite energy) blowups.
:
that exhibits finite time blowup, in which the forcing term
stays uniformly bounded in
for any
.
, which is conducive to generating an exponential “stretching” of a small forcing term at a much higher spatial scale
, which one then introduces to then set up the solution for the next scale.
, where
is a smooth compact manifold, and the metric on
is just the sum of the standard metric
on the first coordinate and
:
, the velocity field
now becomes
, and the Euler equations now split as
,
to the equation
is hidden in this system through the covariant derivative
. To eliminate the metric, we can lower indices to write
and some fields
and
. This particular ansatz seems consistent with all known conservation laws; however it works out to basically be ten vector equations (plus some additional scalar constraints) on ten vector field unknowns, so is just barely overdetermined. I have not been able to locate a self-similar blowup ansatz that is underdetermined.