Pointwise convergence of bilinear polynomial averages over the primes

What's new 2024-09-17

Ben Krause, Hamed Mousavi, Joni Teräväinen, and I have just uploaded to the arXiv the paper “Pointwise convergence of bilinear polynomial averages over the primes“. This paper builds upon a previous result of Krause, Mirek, and myself, in which we demonstrated the pointwise almost everywhere convergence of the ergodic averages

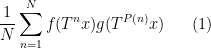
$\displaystyle \frac{1}{N} \sum_{n=1}^N f(T^n x) g(T^{P(n)} x) \ \ \ \ \ (1)$

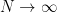
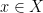
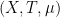
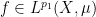
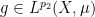
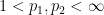
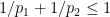
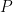
as ${N \rightarrow \infty}$ and almost all ${x \in X}$ , whenever ${(X,T,\mu)}$ is a measure-preserving system (not necessarily of finite measure), and ${f \in L^{p_1}(X,\mu)}$ , ${g \in L^{p_2}(X,\mu)}$ for some ${1 < p_1,p_2 < \infty}$ with ${1/p_1 + 1/p_2 \leq 1}$ , where ${P}$ is a polynomial with integer coefficients and degree at least two. Here we establish the prime version of this theorem, that is to say we establish the pointwise almost everywhere convergence of the averages

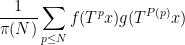
$\displaystyle \frac{1}{\pi(N)} \sum_{p \leq N} f(T^p x) g(T^{P(p)} x)$

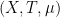
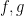
under the same hypotheses on ${(X,T,\mu)}$ , ${f, g}$ . By standard arguments this is equivalent to the pointwise almost everywhere convergence of the weighted averages

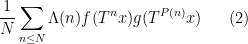
$\displaystyle \frac{1}{N} \sum_{n \leq N} \Lambda(n) f(T^n x) g(T^{P(n)} x) \ \ \ \ \ (2)$

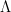
where ${\Lambda}$ is the von Mangoldt function. Our argument also borrows from results in a recent paper of Teräväinen, who showed (among other things) that the similar averages

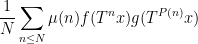
$\displaystyle \frac{1}{N} \sum_{n \leq N} \mu(n) f(T^n x) g(T^{P(n)} x)$

converge almost everywhere (quite fast) to zero, at least if ${X}$ is assumed to be finite measure. Here of course ${\mu}$ denotes the Möbius function.

The basic strategy is to try to insert the weight 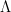${\Lambda}$ everywhere in the proof of the convergence of (1) and adapt as needed. The weighted averages are bilinear averages associated to the bilinear symbol

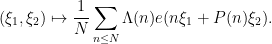
$\displaystyle (\xi_1,\xi_2) \mapsto \frac{1}{N} \sum_{n \leq N} \Lambda(n) e(n \xi_1 + P(n) \xi_2).$

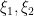
In the unweighted case, results from the additive combinatorics theory of Peluse and Prendiville were used to essentially reduce matters to the contribution where ${\xi_1,\xi_2}$ were “major arc”, at which point this symbol could be approximated by a more tractable symbol. Setting aside the Peluse-Prendiville step for now, the first obstacle is that the natural approximation to the symbol does not have sufficiently accurate error bounds if a Siegel zero exists. 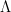While one could in principle fix this by adding a Siegel correction term to the approximation, we found it simpler to use the arguments of Teräväinen to essentially replace the von Mangoldt weight ${\Lambda}$ by a “Cramér approximant”

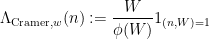
$\displaystyle \Lambda_{\mathrm{Cramer}, w}(n) := \frac{W}{\phi(W)} 1_{(n,W)=1}$

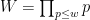
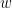
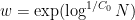
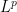
where ${W = \prod_{p \leq w} p}$ and ${w}$ is a parameter (we make the quasipolynomial choice ${w = \exp(\log^{1/C_0} N)}$ for a suitable absolute constant ${N}$ ). 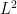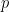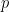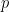This approximant is then used for most of the argument, with relatively routine changes; for instance, an ${L^p}$ improving estimate needs to be replaced by a weighted analogue that is relatively easy to establish from the unweighted version due to an ${L^2}$ smoothing effect, and a sharp ${p}$ -adic bilinear averaging estimate for large ${p}$ can also be adapted to handle a suitable ${p}$ -adic weight by a minor variant of the arguments. The most tricky step is to obtain a weighted version of the Peluse-Prendiville inverse theorem. Here we encounter the technical problem that the Cramér approximant, despite having many good properties (in particular, it is non-negative and has well-controlled correlations thanks to the fundamental lemma of sieve theory), is not of “Type I”, which turns out to be quite handy when establishing inverse theorems. So for this portion of the argument, we switch from the Cramér approximant to the Heath-Brown approximant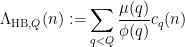

$\displaystyle \Lambda_{\mathrm{HB},Q}(n) := \sum_{q<Q} \frac{\mu(q)}{\phi(q)} c_q(n)$

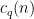
where ${c_q(n)}$ is the Ramanujan sum

$\displaystyle c_q(n) := \sum_{r \in ({\bf Z}/q{\bf Z})^\times} e(-rn/q).$

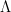
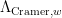
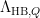
While this approximant is no longer non-negative, it is of Type I, and thus well suited for inverse theory. In our paper we set up some basic comparison theorems between ${\Lambda}$ , ${\Lambda_{\mathrm{Cramer},w}}$ , and ${\Lambda_{\mathrm{HB},Q}}$ in various Gowers uniformity-type norms, which allows us to switch relatively easily between the different weights in practice; hopefully these comparison theorems will be useful in other applications as well.