Generalizations of Nim

Wildon's Weblog 2018-03-12

Probably everyone knows that the P-positions (previous player has won) in Nim are exactly those $(x_1,\ldots,x_r)$ such that $x_1 \oplus \cdots \oplus x_r = 0$ , where $\oplus$ denotes bitwise XOR. For example, $(3,2,1)$ is a P-position, because $3 \oplus 2 \oplus 1 = 11_2 \oplus 10_2 \oplus 01_2 = 00_2 = 0$ , whereas one glance at $(9,7,5,1)$ shows it is an N-position (next player wins), because only the pile of size $9$ contains $2^3$ in binary. Any winning move must take at least $2$ counters from this pile: doing so leaves a pile of size $7 = 4+2+1$ , which is ideal for balancing the contribution $7 \oplus 5 \oplus 1 = 3$ from the other piles. Therefore we leave $3$ counters, taking $6$ , reaching the P-position $(3,7,5,1)$ .

Every finite impartial game is equal to a nimber. Nim is unusual in that knowing the P-positions immediately determines all its nimbers: $(x_1,\ldots,x_r) = m \star$ if and only if $(x_1,\ldots,x_r) + m\star = 0$ (disjoint sum of games) if and only if $(x_1,\ldots,x_r,m)$ is a P-position.

Theorem. The nimber of $(x_1,\ldots, x_r)$ is $(x_1 \oplus \cdots \oplus x_r)\star$ .

Proof. By the previous paragraph, it suffices to find a winning move when $x_1 \oplus \cdots \oplus x_r = 2^s + M$ with $M < 2^s$ . By induction, we may assume that all options of $(x_1,\ldots,x_r)$ have their expected nimbers. By reordering piles we may assume without loss of generality that $x_1 = 2^{s+1}A + 2^s + B$ where $A \in \mathbb{N}_0$ and $B < 2^s$ . We take all but $2^{s+1}A + 2^s-1$ counters from the first pile, pause to admire the situation, and then take further counters to leave exactly $2^{s+1}A + (2^{s+1}A \oplus x_2 \oplus \cdots \oplus x_r)$ . The parenthetical quantity is

$2^s \oplus B \oplus x_1 \oplus \cdots \oplus x_r = 2^s \oplus B \oplus 2^s \oplus M = B \oplus M < 2^s,$

so this is always possible. $\Box$

A small generalization of this argument finds explicit moves giving options of $(x_1,\ldots,x_r)$ with all nimbers $m' \star$ with $m' < x_1 \oplus \cdots \oplus x_r$ .

Example. Before I learned about Combinatorial Game Theory I got thrashed at Nim by someone whose main tactic was to reduce to the zero position $(3,2,1)$ . (Of course my opponent could also win any non-balanced position with two piles.) In memory of this occasion, consider the position $(19,13,3,2,1) = 19\star + 13\star = 30 \star$ . To reach $(16 + c) \star$ with $0 \le c \le 7$ , we observe that $30$ and $16 + c$ both have $16$ in their binary expansion, but only $30$ has $8$ (present in the pile $13$ ). We mentally cancel out the $16$ s, leaving $(3,13,3,2,1)$ with target $s \star$ , and play, as a first step, to $(3,7,3,2,1)$ . We then calculate that

$3 \oplus 3 \oplus 2 \oplus 1 \oplus c = 3 \oplus c.$

We must leave $3 \oplus c$ counters in the half-eaten pile of size $7$ ; since $0 \le c \le 7$ , this is always possible. For instance, if $c = 5$ then since $3 \oplus 5 = 6$ , we leave $6$ counters. Since $3 \oplus 6 \oplus 3 \oplus 2 \oplus 1 = 6$ , on restoring the cancelled subpiles, we reach a position of nimber $(19 \oplus 6 \oplus 3 \oplus 2 \oplus 1)\star = 21 \star$ , as required.

Strong players of games instinctively maximize their mobility. This principle gives a decent strategy for games ranging from Settlers of Catan (a resource acquisition game in which early mobility is essential) and Othello (in which weak players often minimize their mobility, by playing to maximizing their counters in the early game; typically this creates multiple good moves for the opponent) and even a reasonable heuristic for chess, albeit one that has been criticized by Turing. It can be seen at work in the proof and example above, where the half-eaten pile of size

$\begin{aligned} 2^{s+1}A + 2^s-1 &= 2^{s+1}A + 1 + 2 + \cdots + 2^{s-1} \\ &= 2^{s+1}A \oplus 1 \oplus 2 \oplus \cdots \oplus 2^{s-1} \end{aligned}$

gives us ample options.

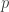$p$ -Nim

Nim boils down to a fight over the nimber $x_1 \oplus \cdots \oplus x_r$ . With the end firmly in mind, let us ask for a generalization in which $\oplus$ is replaced with $\oplus_p$ , the analogue of $\oplus$ defined with addition modulo $p$ . For instance,

$12 \oplus_3 3 \oplus_3 2 \oplus_3 1 = 110_3 \oplus_3 010_3 \oplus_3 002_3 \oplus_3 001_3 = 120_3 = 15,$

and in the hoped for generalization, $(12,3,2,1)$ will have nimber $15{}\star$ and (this is just a restatement) options with nimbers $0,\star,\ldots, 14{}\star$ , but not $15{}\star$ . Consider the option $9\star$ . This can be reached only by removing $3$ counters from both the piles of sizes $12$ and $3$ . So it seems we have to permit moves in multiple piles. The position $(1,1,\ldots,1)$ with $p-1$ singleton piles shows that moves in up to $p-1$ piles may be required. So, as a first try, we make the following definition.

Definition. Naive $p$ -Nim is the impartial game in which each move consists of up to $p-1$ moves in Nim.

Thus, writing $d$ for Hamming distance, a position $x \in \mathbb{N}_0^r$ in naive $p$ -Nim has $y \in \mathbb{N}_0^r$ as an option if and only if $y_i \le x_i$ for each $i$ and $1 \le d(x,y) \le p-1$ .

Suppose, inductively, that the options of $(x_1,\ldots, x_r)$ have the required nimbers. Then $x$ has as options all $m' \star$ with $m' < m$ .

Sketch proof. Take $s$ maximal such that $p^s$ appears more often in $m$ than $m'$ . Cancelling as in the example, we may assume that $p^s$ is the greatest power of $p$ appearing in the base $p$ -forms of $x_1, \ldots, x_r$ . So $m = ap^s + \cdots$ and $m' = a'p^s + \cdots$ . Take $a-a'-1$ subpiles $p^s$ from piles containing $p^s$ in $p$ -ary, and in a remaining pile of size $\alpha p^s + B$ take all but $(\alpha-1)p^s + p^s-1$ of its counters; then use its subpile of size $(p-1) + (p-1)p + \cdots + (p-1)p^{s-1}$ to reach $m' \star$ . $\Box$

However, $(x_1,\ldots, x_r)$ may well have further options. By the mex rule, the problem occurs when there is an option $(y_1,\ldots,y_r)$ with $y_1 \oplus_p \cdots \oplus_p y_r = x_1 \oplus_p \cdots \oplus_p x_r$ . For instance, $(3,2,1)$ has the option $(3,0,0)$ , which has nimber $3 \star$ . This destroys the inductive foundations for the sketch proof above. In fact $(3,2,1) = 6\star$ in naive $3$ -Nim.

The obvious fix is to bar all moves taking counters $[c_1,\ldots,c_r]$ in which $c_1 \oplus_p \cdots \oplus_p c_r = 0$ . (The square brackets are used to distinguish moves from positions.) But still there are too many options: for instance $(6,3)$ should be a P-position with nimber $0$ but, according to the current rules, we can move by $[4,2]$ or $[5,1]$ to the P-positions $(2,1)$ and $(1,2)$ (which really do have nimber $0$ ). A computer search finds the following illustrative examples, listed with their intended nimber and the additional moves that must be made illegal:

$(3,6), 0, \{[2,4],[1,5]\}$ ,
$(3,7), 1, \{[2,7],[1,5]\}$ ,
$(4,8), 0, \{[2,7]\}$ ,
$(5,6), 2, \{[5,4],[4,5]\}$ ,
$(5,7), 0, \{[4,5]\}$ ,
$(6,6), 3, \{[5,1],[4,2],[2,4],[1,5]\}$
$(1,5,7), 1, \{[0,4,5]\}$ ,
$(2,3,7), 0, \{[2,1,0],[2,2,2]],[0,2,7],[0,1,5]\}$ .

Let $v_p(x)$ denote the highest power of $p$ dividing $x \in \mathbb{N}$ , and let $v_p(0) = \infty$ . Some inspection of these examples may suggest the following definition.

Definition. $p$ -Nim is naive $p$ -Nim barring any move taking counters $[c_1,\ldots,c_r]$ such that

$v_p(c_1 \oplus_p \cdots \oplus_p \cdots \oplus_p c_r) > \mathrm{min} \{v_p(c_1), \ldots, v_p(c_r) \}.$

By the definition of $v_p(0)$ , this generalizes our first attempted rule. Moreover, it bars any move not changing the purported nimber $x_1 \oplus_p \cdots \oplus_p x_r$ of $(x_1,\ldots,x_r)$ . The following result is a corollary of Lemmas 3.1 and 3.2 in this paper of Irie.

Theorem [Irie] The nimber of the $p$ -Nim position $(x_1,\ldots,x_r)$ is $(x_1 \oplus_p \cdots \oplus_p x_r)\star$ .

Proof. Let $m = x_1 \oplus_p \cdots \oplus_p x_r$ and let $m' < m$ . Let $p^b = \nu_p(m-m')$ and let $p^s$ be the greatest power of $p$ appearing in $m-m'$ in $p$ -ary. Cancelling as before, we may assume that $p^s$ is the greatest power of $p$ appearing in the base $p$ -forms of $x_1, \ldots, x_r$ . Similarly, we may cancel the powers $p^a$ with $a < b$ between $m$ and $m'$ . So the only powers of $p$ that appear are between $p^b$ and $p^s$ . (This will guarantee that our move satisfies the valuation condition.) Now play as in the sketch proof, replacing $p^s - 1$ with

$p^s - p^b = (p-1)p^b + (p-1)p^{b+1} + \cdots + (p-1)p^{s-1}.$

Since $m \star$ is not an option of $(x_1,\ldots,x_r)$ , the mex rule implies that the nimber of $(x_1,\ldots,x_r)$ is $m \star$ , as required. $\Box$

In fact Irie’s result is more general: a surprising effect of the valuation condition is that allowing moves in $p$ or more piles does not create options with new nimbers. This leads to the notion of the $p$ -saturation of a game. The main focus of Irie’s paper is the $p$ -saturation of Welter’s game, which is shown to have a remarkable connection with the representation theory of the symmetric group.

Back to naive 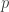$p$ -Nim

It seems that in many cases the nimbers in naive $p$ -Nim are given by ordinary (naive?) addition. For example, this is true for all $k$ -pile positions whenever $p > k$ . When $p =3$ , the exceptions for $3$ pile positions (in increasing order) with a small first pile are listed below.

$(1,x,y)$ : $(1,1,1) = 0$ ,
$(2,x,y)$ : $(2,2,2) = 0, (2,2,3) = \star$ ,
$(3,x,y)$ : $(2,2,3) = \star, (3,3,3) = 0, (3,3,4) = 2\star$ ,
$(4,x,y)$ : $(3,3,4) = 2\star, (4,4,4) = 0, (4,4,5) = \star, (4,4,6) = 3\star$ , $(4,5,5) = 3\star$ .