Collisions in Greg Egan’s Orthogonal physics

Wildon's Weblog 2021-04-12

In Greg Egan’s remarkable Orthogonal Trilogy, physics differs from ours in one crucial respect: the Lorentz metric $c^2\mathrm{d}t^2 - \mathrm{d}\mathbf{x}^2$ is replaced with the Riemannian metric $\mathrm{d}t^2 + \mathrm{d}\mathbf{x}^2$ , putting time on the same footing as distance. As one would expect from this author, the consequences are worked out in great detail, and are integral to the plot. This comes at some predictable expense to characterisation and versimilitude: still I’ve found the first two books sufficiently interesting that I can (almost) ignore that most of the exposition consists of the characters giving each other physics tutorials, conducting experiments (which remarkably always work, even if the results often come as a surprise) or listening to each other give lectures and seminars. `I wanted to write a physics textbook, but the publisher made me write this science fiction trilogy instead’.

The purpose of this post is to do one of the exercises left implicitly to the reader in the second book, The Eternal Flame, in which it is observed that when a photon is deflected by a stationary particle of ordinary matter (called a `luxagen’ in the trilogy), it may glance off at two different angles. Moreover, there is a maximum deflection angle, which is independent of the energy of the photon.

Here I’ll show that this follows from the relation between energy and momentum in Orthogonal physics, and the two conservation laws, and implies that Orthogonal photons are heavier than luxagens. I’ll also show that the same behaviour holds in our universe, whenever the moving particle is heavier than the particle it strikes. Much of the interest arises from how Egan (and his characters) arrive at this setup: for more background see the supplementary material on Egan’s website, or read the first book in the trilogy, The clockwork rocket.

Space-time and the energy-momentum relation

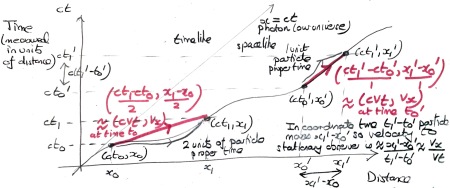
There is $4$ -dimensional space-time. In our universe, when we measure a time interval $T$ by the distance $cT$ that light travels in this interval, space-time has the Lorentz metric $c^2 \mathrm{d}t^2 - \mathrm{d}x^2 - \mathrm{d}y^2 - \mathrm{d}z^2$ . For example, a photon may move from $(0,0,0,0)$ to $(1,c,0,0)$ in one unit of time, and, corresponding to the fact that no time passes for the photon, the Lorentz distance between these space-time points is zero. In the Orthogonal universe space-time has the Riemannian metric $k^2 \mathrm{d}t^2 + \mathrm{d}x^2 + \mathrm{d}y^2 + \mathrm{d}z^2$ , where $k$ is a constant with dimension distance/time; by choosing units appropriately (thus sweeping under the carpet the first half of the first book on Yalda’s experiments on Mount Peerless, the beautiful dual Pythagorean Theorem, and the fact that in Orthogonal physics, the speed of light is not constant), we may assume that the numerical value of $k$ is $1$ . We take the following (and only the following, for the time being) as further axioms:

Physical laws are invariant under the group of transformations preserving the Lorentz/Riemannian metric.
Every particle has a symmetry invariant tangent vector $(cv_t,v_x,v_y,v_z)$ to its world line called its $4$ –velocity with units distance/time; a stationary observer measures the particle’s velocity as the $3$ -vector $(v_x,v_y,v_z)/cv_t$ , as illustrated in the diagram below. Click on the diagram for a larger pdf.
Multiplying the $4$ -velocity, normalized to have length $c$ (our universe) or $1$ (the Orthogonal universe), by the mass $M$ of a particle gives its $4$ -momentum $(E/c, \mathbf{p})$ , where $\mathbf{p}$ is the $3$ -vector momentum.

Note that (1) only makes sense because we measure time and distance in compatible units: thus whenever a time, such as $t_1$ in the diagram above appears, it is multiplied by $c$ . Therefore the symmetry group of space-time can reasonably mix them up.

The way I imagine (2), half-remembered from when I did special relativity 20 years ago (my reference frame) is that the $xt$ -plane has clocks every metre, connected by rigid rods, which record the time of passing of every particle. The particle is at position $x_0$ (which conveniently enough happens to have a clock) at time $ct_0$ , and at position $x_1$ (similarly conveniently placed) at time $ct_1$ . The stationary observer can therefore collect the measurements from the clocks (simply by travelling to each one), and approximate the particle’s velocity as $(x_1-x_0)/c(t_1-t_0)$ and so $v_x/v_t \approx (x_1-x_0)/c(t_1-t_0)$ . Everyday objects in our universe, such as cars, trains and coronavirus, move at a negligible fraction of the speed of light, so $c(t_1-t_0)$ is typically huge compared to $x_1-x_0$ , and corresponding the velocity measured by the observer is a tiny fraction of the speed of light.

(Note this is not the velocity that an observer travelling with the particle would measure: this requires the notion of proper time; this is the usual way to define the $4$ -vector velocity, but except for the informal diagram above, we’re not going to use it here.)

More generally, writing $\mathbf{v}$ for the $3$ -velocity, and as usual in physics, $\mathbf{v}^2$ for its $3$ -vector Euclidean norm $||v|| = \sqrt{v_x^2+ v_y^2+v_z^2}$ , (2) implies that $(cv_t,v_x,v_y,v_z) = (cv_t, \mathbf{v}v_t)$ . By symmetry invariance, the Lorentzian norm squared of the tangent vector is $(c^2 - \mathbf{v}^2) v_t^2$ , and the Euclidean norm squared is $(1+\mathbf{v}^2)v_t^2$ (using the assumption that $k=1$ ). Now since $(c^2 - \mathbf{v}^2)v_t^2$ has units distance/time, and we care only about the direction of the tangent vector, not its magnitude, it is most convenient (and usual in physics, although I’ve never seen it clearly explained why) to require that the Lorentzian length is $c$ .

Thus in our universe $(c^2-\mathbf{v}^2)v_t^2 = c^2$ , and so $v_t = c/\sqrt{c^2-\mathbf{v}^2} = 1/\sqrt{1-\mathbf{v}^2/c} = \gamma(\mathbf{v})$ , where $\gamma(\mathbf{v})$ is the usual dimensionless Lorentz factor. In the Orthogonal universe $v_t = 1/\sqrt{1+v^2}$ ; this is again dimensionless because the $1$ in the numerator implicitly has units distance/time.

Therefore the $4$ -vector velocity is

$\displaystyle (cv_t,v_x,v_y,v_z) = (c\gamma(\mathbf{v}), \mathbf{v}\gamma(\mathbf{v}) ) = \bigl(\frac{c}{\sqrt{1-\mathbf{v}^2/c^2}}, \frac{\mathbf{v}}{\sqrt{1-\mathbf{v}^2/c^2}}\bigr)$

in our universe and

$\displaystyle \bigl(\frac{1}{\sqrt{1+\mathbf{v}^2}}, \frac{\mathbf{v}}{\sqrt{1+\mathbf{v}^2}} \bigr)$

in the Orthogonal universe.

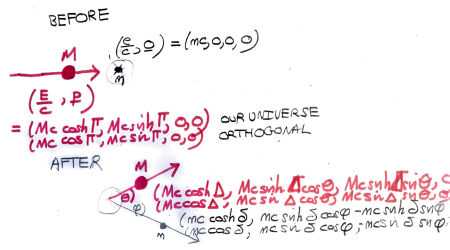
According to (3) the familiar $3$ -vector momentum is obtained by multiplying the spatial component of each of these $4$ -vector velocities by the rest mass $M$ . In our universe, this agrees with special relativity: a particle moving at $3$ -vector velocity $\mathbf{v}$ is heavier according to a stationary observer by the factor $\gamma(\mathbf{v})$ . In the Orthogonal universe, we find instead that the $3$ -vector momentum is $M\mathbf{v}/\sqrt{1+\mathbf{v}^2}$ , so fast moving particles are lighter according to a stationary observer.

Again by (3), the energy $E$ of the particle is given by $E/c = Mc \gamma(\mathbf{v})$ in our universe, and $E = M/\sqrt{1-\mathbf{v}^2}$ in the Orthogonal universe. Substituting in the $4$ -vectors, we find that in our universe $(E/c, M\gamma(\mathbf{v})\mathbf{v})$ has Lorentzian length $Mc$ , and in the Orthogonal universe, $(E, M\mathbf{v}/\sqrt{1+\mathbf{v}^2})$ has Euclidean length $M$ . Equivalently, energy and momentum are related in our universe by

$(E/c)^2 - \mathbf{p}^2 = M^2c^2$

and in the Orthogonal universe by

$E^2 + \mathbf{p}^2 = M^2.$

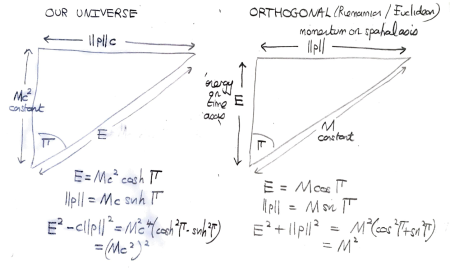
The former is one statement of the energy-momentum relation between the energy $E$ and the $3$ -momentum $\mathbf{p}$ . Observe that the Orthogonal energy-momentum relation can be stated very neatly as $E = M \cos \Gamma$ and $|| \mathbf{p} || = M \sin \Gamma$ , where $\Gamma \in [0, \pi/2]$ . The analogue for our universe, using the identity $\cosh^2 \Gamma - \sinh^2\Gamma = 1$ , is $E = Mc^2 \sinh \Gamma$ and $||\mathbf{p} || = Mc \cosh \Gamma$ . We show both by the triangles below, noting that only the Orthogonal triangle is a genuine geometric representation, rather than a helpful aide-memoire.

Collision setup

We now need one final pair of axioms

In any system of particles, the sum of all $3$ -vector momenta is conserved;
In any system of particles, the sum of all energies (as recorded in the time component of $4$ -vector momenta) is conserved.

The diagrams below show a stationary particle with mass $m$ hit by a heavy particle with mass $M$ moving in the $x$ direction (and also in time, of course). Again click on the diagram for a larger pdf.

We can suppose that after the collision motion is contained in the $txy$ -plane, so all $z$ -coordinates are zero: let $\phi$ and $\theta$ be the deflection angles of the lighter and heavier particle. The $4$ -momenta conservation equations are, in our universe,

$\begin{aligned} mc + Mc \cosh \Gamma &= mc \cos \delta + Mc \cos \Delta \\ Mc \sinh \Gamma &= mc \sinh \delta \cos \phi + Mc \sinh \Delta \cos \theta \\ 0 &= -mc \sinh \delta \sin \phi + mc \sinh \Delta \sin \theta. \end{aligned}$

Notice that these are homogeneous in $c$ . We can therefore divide through by $c$ and write a unified system of equations for both our universe and the Orthogonal universe as

$\begin{aligned} T &= m\, \mathrm{co}\ \delta + M\, \mathrm{co}\ \Delta \\ (T-m)\, \mathrm{ta}\ \Gamma &= m\, \mathrm{si}\ \delta \cos \phi + M\, \mathrm{si}\ \Delta \cos \theta \\ 0 &= -m\, \mathrm{si}\ \delta \sin \phi + M\, \mathrm{si}\ \Delta \sin \theta \end{aligned}$

where $\mathrm{co}, \mathrm{si}, \mathrm{ta}$ denote $\cosh, \sinh, \tanh$ for our universe and $\cos, \sin, \tan$ for the Orthogonal universe. Note that $m$ , $M$ and $\Gamma$ , which appear only on the left-hand side, are constant and are determined by the experimental setup; the unknowns are $\delta$ , $\Delta$ , $\phi$ and $\theta$ .

It is routine to solve these equations numerically using NSolve in Mathematica. As an example, we suppose that the heavier particle has three times the mass of the lighter, so $m/M = 1/3$ . The graph below show the post-collision velocity $V$ of the heavier particle for each of the two possible deflection angles $\theta$ , as the energy of the heavier particle increases from least (red) to greatest (violet).

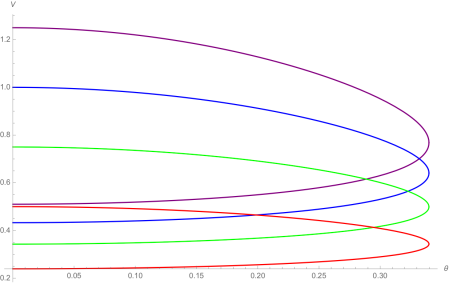
This agrees with the experiment conducted in Orthogonal where the heavier particle is a photon, and the characters observe the deflection angle by visual observation of a system of mirrors. The graph below the has the same axes, comparing the post-collision velocity in the Orthogonal universe (solid) and our universe (dashed), choosing the energies to get comparable shapes. Notice that the maximum deflection angle does not depend on the energy of the heavier particle, or on which universe we are in: we show below that its sine is the ratio of the masses. Thus in these graphs it is $\sin^{-1} 1/3 \approx 0.33984$ .

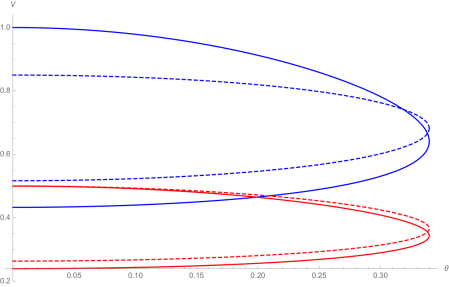
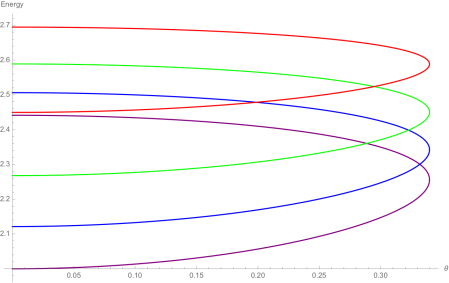
The graph below is the equivalent of the first graph showing the final energy of the heavier particle. If you are surprised that red is now at the top, note that in Orthogonal physics, the energy is $M/\sqrt{1+V^2}$ , so is lower for faster moving particles.

Tangent space equation

Differentiating the second and third equations above we get to be concluded.