Q is for quantum

The purpose of this post (in progress as of late October 2021) is to serve partly as a review of Terry Rudolph’s book Q is for quantum and partly as a record of my thoughts after a few months of reading about quantum computation. The first part of Ruldolph’s book can be freely downloaded from his website.

Part 1: Q-computing

Q is for quantum begins with a version of the Stern–Gerlach experiment. We are asked to imagine that black and white balls are sent through a box called ‘PETE’: the afterword makes clear the name comes from a collaborator of Rudolph. After a black ball goes through PETE, it is observed to be equally likely to be black and white. The same holds for white balls.

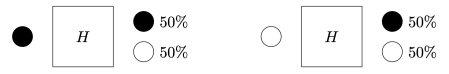
Moreover, the black balls that come out are indistinguishable by any physical experiment from the black balls that come in, and the same holds for white balls. For example, if the white balls coming out are discarded, and the black balls passed through a second PETE box, then again the output ball is equally likely to be black and white.

But if two PETE boxes are connected so that a white ball put into the first one passes immediately into the second, the output is always white.

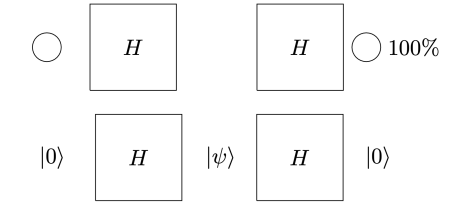
Naturally we are suspicious that, despite our earlier failure to distinguish balls output from PETE boxes from fresh balls, the first PETE box has somehow ‘tagged’ the input ball, so that when it goes into the second box, the second PETE box knows to output a white ball. When we test this suspicion by observing the output of the first PETE box, we find (as expected) that the output of the first box is 50/50, but so is the output of the second. Somehow observation has changed the outcome of the experiment.

This should already seem a little surprising. But if we accept that observed balls coming out of PETE are experimentally indistinguishable from fresh balls then, as Rudolph persuasively argues, we have to make a more radical change to our thinking: there is no way to interpret the state of an unobserved ball midway between two PETE boxes as either black or white. As Rudolph says, ‘We are forced to conclude that the logical notion of “or” has failed us’. This quickly leads to an informal idea of superposition and Rudolph’s central concept of a misty state. For example, the state shown above is drawn as the diagram below.

Rudolph then makes the bold step of supposing that when a black ball, represented by is put through PETE, the output is ; of course this is drawn in his book as another misty state, this time with a minus sign attached to the black ball. Does this contradict the experimental indistinguishability of output balls? Not according to Rudolph:

It isn’t a “physically different” type of black ball: if we looked at the ball at this stage we would just see it as randomly either white or black. No matter what we do, we won’t be able to see anything to tell us that when we see it as black it is actually “negative black”

In the mathematical formalism, this is the unobservability of a global phase: something one must accept as an exiom. Rudolph’s explanation of this point is characteristically clear. The behaviour of a white ball sent into two PETE boxes in immediate succession is easily explained using superposition: Rudolph’s ‘misty’ diagram on page 20 becomes the following calculation:

It is an impressive feature of Rudolph’s book that he is able to use the PETE box and his misty state diagrams to illustrate many of the key ideas in quantum computation. It is of course a routine translation to pass to the usual bra/ket formalism. As one might hope, this infusion of mathematics has some advantages. For instance, we can now require that states evolve by unitary transformations, making the ‘bold’ step above intuitive: once we know that , unitary dynamics require that . Thus, as my notation in the diagrams above suggests, the PETE box is the Hadamard gate

If Rudolph’s white/black ball thought experiments and the associated formalism have a weakness, I think it may be more physical than mathematical.

For instance, the Stern–Gerlach experiment was first performed with silver atoms: the atomic number of silver is , and correspondingly there is a single electron in the 4f subshell, whose spin can be detected by passing the atoms through a magnetic field. Thus silver atoms replace balls and magnetic fields replace the PETE boxes. Using further magnetic fields one can separate the spin-up post-PETE atoms from the spin-down post-PETE atoms, and then send the atoms on separate journeys: if at the end they meet up (without observation at any stage), the same interference occurs, and the output is always spin-down. To stretch the analogy this far, Rudolph would have had to introduce some machine that separated the two colours, potentially confusing the story. (Why does observation by the machine not destroy the interference pattern?)

Further effects, for example that spin-up atoms are (essentially by definition) deflected up by up/down magnetic fields, but are equally likely to go either way in a left/right magnetic field, have no analogue at all. But Rudolph has already made a convincing (and entirely honest) case that quantum phenomena cannot be understood by classical physics or conventional probability.

Incidentally, I highly recommend this MIT lecture by Allan Adams for an entertaining treatment of the Stern–Gerlach experiment that has some features in common with Rudolph’s presentation, for instance, the use of colour to replace spin.