Dominic Welsh, 1938–2023

Gödel’s Lost Letter and P=NP 2024-03-26

My doctoral thesis advisor

Geoffrey Grimmett source

Dominic Welsh passed away last November 30th. He was my doctoral advisor 1981–86 at Merton College, Oxford University, and a giant in several fields of combinatorial and applied mathematics.

Today I remember Dominic and describe his late-career influence on a modern problem: How “natural” is bounded-error quantum polynomial time?

Among several memorials by colleagues and friends, there is now a detailed tribute on the Matroid Union blog by my fellow student and Oxford officemate Graham Farr with fellow students Dillon Mayhew and James Oxley. Graham lays out the full variety of Dominic’s career, beginning with his work on discrete probability and then going on to matroid theory—work that led him to write the definitive text Matroid Theory already in 1976.

I first met Dominic on a visit to Oxford in August 1980, on my way back from playing chess in Norway. This was a month before the start of my senior year at Princeton and decision to apply for a Marshall Scholarship. I was beginning an undergraduate thesis on algebraic combinatorics supervised by Doug West and Harold Kuhn. Although I had attended some talks on computational complexity, including one by Eugene Luks on isomorphism for graphs of bounded degree being in ${\mathsf{P}}$ , I had not thought of doing complexity as a research area of itself until I arrived to Merton College in September 1981. Dominic was so enthusiastic about complexity that I never heard much about matroid theory from him; ironically I have come to that subject only fairly recently.

Computational Complexity and Physical Systems

Dominic’s view on complexity came from statistical physics, a subject proceeding from his own doctoral thesis in 1964 under John Hammersley. He was most interested in counting problems. Leslie Valiant had recently introduced the complexity class ${\mathsf{\#P}}$ and shown that computing the permanent of a matrix is ${\mathsf{\#P}}$ -complete, hence ${\mathsf{NP}}$ -hard. The problems of counting satisfying assignments, graph 3-colorings, Hamiltonian cycles, and perfect matchings in bipartite graphs are also ${\mathsf{\#P}}$ -complete.

The first three are counting versions of ${\mathsf{NP}}$ -complete decision problems, but the decision version of the last—does a graph have a perfect matching?—belongs to ${\mathsf{P}}$ . The counting problem ${\mathsf{\#2SAT}}$ for clause size ${k=2}$ is ${\mathsf{\#P}}$ -complete, even though ${\mathsf{2SAT}}$ is in ${\mathsf{P}}$ .

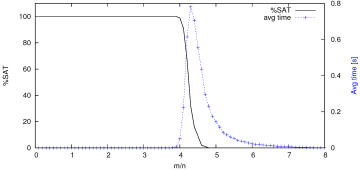
What fascinated Dominic even more was that instances of the hard problems can often be structured with a natural parameter ${p}$ so that the complexity transitions from easy to hard in a narrow critical region as ${p}$ varies. The classic example is the ratio of clauses to variables in ${k}$ -SAT instances and other forms of constraint satisfaction. Here is a diagram for 3SAT from a 2013 paper by Marcelo Finger and Poliana Reis, showing both the probability of being satisfiable and the time taken by an exhaustive algorithm:

For graph coloring and Hamiltonian cycles one can use parameters that govern the distribution for drawing random graph instances. The meta-question here is:

If in fact ${\mathsf{P=NP}}$ , then what accounts for this observed phenomenon of sharp phase transition in evident hardness?

See this 2012 talk by Cris Moore with hints on how further phase phenomena could possibly unlock ${\mathsf{P \neq NP}}$ . Stepping back to the early 1980s, all this raised early hope that the theory of physical systems, such as the Ising model, could help surmount barriers to complexity lower bounds that were already being felt.

Percolation and a Story

The world has just been through a long engagement with a phase-transition parameter, the reproduction number ${R_0}$ of an epidemic. It is normalized so that if ${R_0 < 1}$ then the infection will be contained in ideal circumstances, but if ${R_0 > 1}$ it will almost certainly pervade the population.

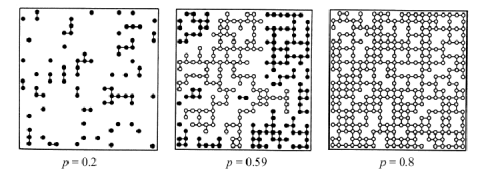
Dominic introduced me to related examples in percolation theory that were not causing actual disasters. Open problems emerge almost immediately. Consider ${n\times n}$ square lattices in which every node is independently colored black with probability ${p}$ . There is a critical value ${p_c}$ such that when ${p < p_c}$ , the probability of having a path of black nodes span the lattice goes to ${0}$ sharply as ${n \rightarrow \infty}$ , but for ${p > p_c}$ the probability of a spanning black cluster is nonzero and ramps up quickly. This value has been empirically computed as ${0.59274621 \pm 0.00000013}$ but is not known analytically.

Paul Heitjans source

I was duly warned that analytic bounds on ${p_c}$ for other families of grids were as hard to do as complexity lower bounds. Dominic and Paul Seymour had made important progress on the problem for edges in the square lattice, which had helped Harry Kesten prove ${p_c = 0.5}$ for them in 1980. (See also this 2022 paper.) Thresholds for many other lattice structures have been computed empirically but remain open analytically.

My strongest memory of percolation in my first year had a different purpose. Much work was being done by physicists whose level of rigor was below standard. Dominic set me to probe one such paper, and I confirmed his suspicion of a major gap in the main result. Rather than send a letter, he invited the author over to Oxford, and after suitable entertainment at Fellows Lunch, brought him to meet me at the Mathematical Institute. Having prepped the approach with me beforehand, and with his usual twinkle in the eyes, he invited the author to lay out his proof. I posed questions that led to the flaw, and the poor chap was duly flustered—but appreciative at the same time. At least he was treated in best fashion.

Complexity

I took the mindset, however, that hope of progress in complexity needed not only greater rigor but a full embrace of logic and formal structures. I was primed to be caught up in the Structural Complexity movement of the 1980s, which enshrined the field’s main conference until it was renamed the “Computational Complexity Conference” in 1996. Among papers I studied on the possible independence of ${\mathsf{P}}$ versus ${\mathsf{NP}}$ from strong formal systems was this by Dick with Rich DeMillo.

This went outside Dominic’s interests, but his steady and kindly hand was important especially through a tumultuous fourth year for me. During that fourth year, we co-taught a course on complexity, communication, and coding theory, which figured into his 1988 textbook Codes and Cryptography. Here is the end of its preface:

As for doing something about “hieroglyphic handwriting,” I brought in the inexpensive PC-based typesetting system ${T^3}$ (now Scientific Word) with the generous support of the Mathematical Institute, where it was housed in room T-3. I manually improved all the ${24 \times 18}$ pixel math-and-language fonts, which had evidently been digitized rather than crafted, so I joked that I had “written” a dozen dissertations before I finished mine the next year.

My camera, Merton College, October 1986 (AI-enhanced)

Capturing BQP

Between then and Dominic’s 2005 retirement, he branched into new strands of complexity involving graph and knot polynomials, which grew into and beyond his 1993 book Complexity: Knots, Colorings, and Countings. (Although this is by Cambridge University Press, I have added an Oxford comma to the title.) This fostered a connection to quantum computing via the Jones polynomial of knot theory. The basic relation was discovered by Michael Freedman, Alexei Kitaev, Michael Larson, and Zhenghan Wang in their foundational 2003 paper “Topological Quantum Computing”:

Theorem 1 (paraphrase) In time polynomial in the size ${s}$ of a given quantum circuit ${C}$ , an argument ${x}$ to ${C}$ , and ${\log(1/\epsilon)}$ , we can create a knot link ${L}$ and a simple formula ${g_L}$ such that
$\displaystyle \left|\Pr[C(x)=1] - g_L(V_L(e^{2\pi i/5}))\right| < \epsilon,$
where ${V_L}$ is the Jones polynomial of ${L}$ .

In contrast to polynomial translations I’ve discussed here and here, there is only one evaluation of the Jones polynomial—and at a “magic” fifth root of unity.

Now Dominic—with his student Dirk Vertigan and with François Jaeger of Grenoble—showed that evaluating ${V_L}$ at any point other than a ${2,3,4,6}$ th root of unity is ${\mathsf{\#P}}$ -hard given general ${L}$ . Many other problems that express the evaluation of quantum circuits are likewise ${\mathsf{\#P}}$ -hard, including some of the special cases shown here. This raises a natural meta-question:

Is it possible to simulate ${\mathsf{BQP}}$ via a natural computational problem that is not (known to be) ${\mathsf{\#P}}$ -hard on its full natural domain of instances?

There is a case to be made for a categorical no answer. The dichotomy phenomenon is that whole classes ${C}$ of natural functions ${f}$ in ${\mathsf{\#P}}$ have the property that every ${f \in C}$ is either in ${\mathsf{P}}$ or is ${\mathsf{\#P}}$ -complete. Now ${\mathsf{BQP}}$ is believed to be intermediate between ${\mathsf{P}}$ and ${\mathsf{PP}}$ , the latter being the language-class peer of ${\mathsf{\#P}}$ . But dichotomy seems to leave no room for a natural capture of ${\mathsf{BQP}}$ that stays in-between. This is besides the observation from structural complexity theory that insofar as ${\mathsf{BQP}}$ is a “promise” class, it is unlikely to have a complete decision problem, nor ipso facto be captured by simple function computations.

An Answer

Dominic’s 2005 paper with Freedman, Laci Lovász, and Dominic’s student Magnus Bordewich gave—among several results—a task that exactly captures ${\mathsf{BQP}}$ . This required a clever new condition of approximation for numerical functions ${f}$ . The most familiar ones require computing (deterministically or with high probability) a value ${y}$ such that

$\displaystyle f(x) - \epsilon f(x) \leq y \leq f(x) + \epsilon f(x),$

where for every prescribed ${\epsilon > 0}$ , the running time is polynomial in ${|x|}$ . If the time is also polynomial in ${\frac{1}{\epsilon}}$ , one speaks of a fully approximating scheme (FPRAS in the random case).

A rub with this is that the most familiar numerical approaches to simulating quantum circuits ${C}$ make the acceptance probability (or variously, the amplitude) have the form

$\displaystyle \Pr[C(x)=1] = \frac{f_1(x) - f_2(x)}{R},$

where ${f_1}$ and ${f_2}$ are fully approximable but the difference ${f_1(x) - f_2(x)}$ is small, typically of order ${(f_1(x) + f_2(x))^{1/2}}$ . This “multiplicative” approximation property does not carry through to the difference.

Their additive approximation scheme takes an auxiliary function ${u(x)}$ and seeks to compute ${y}$ such that

$\displaystyle f(x) - \epsilon u(x) \leq y \leq f(x) + \epsilon u(x). \ \ \ \ \ (1)$

Now if ${f_1(x)}$ and ${f_2(x)}$ are approximable with “normalizer” ${u(x)}$ in this sense, then so is ${f_1(x) - f_2(x)}$ with normalizer ${2u(x)}$ . This works even if the difference is relatively tiny as above, provided ${u(x)}$ is chosen appropriately. It still took more cleverness and an appeal to knot theory to make the idea work for ${\mathsf{BQP}}$ :

Theorem 2 (paraphrase) Let ${A}$ be an oracle function that takes as input ${\epsilon}$ and a knot link ${L}$ , where ${L}$ is given as the plat closure of a braid of string size ${m}$ , and returns an additive approximation of ${V_L(e^{2\pi i/5})}$ within ${\epsilon}$ times the normalizer ${(2\cos\frac{\pi}{5})^{m/2}}$ . Then ${\mathsf{BQP = P^A}}$ .

Here ${L}$ is the “ ${x}$ ” in the definition of additive approximation. In words, the task of generating such approximations of the Jones polynomial at a fifth root of unity is equivalent in power to ${\mathsf{BQP}}$ , allowing only deterministic polynomial time computation otherwise. As the tribute co-written by Graham Farr puts it,

Dominic collaborated with Bordewich, Freedman and Lovász on an important paper (2005) showing that an additive approximation (which is weaker than an FPRAS) to a certain Tutte polynomial evaluation (related to the Jones polynomial) is sufficient to capture the power of quantum computation. (emphasis added)

Dominic had much more engagement with quantum computing, including his co-supervision with Artur Ekert of Michele Mosca, who went on to the University of Waterloo and was one of several who welcomed Dominic there for an honorary doctorate in 2006.

Open Problems

The Matroid Union tribute mentions numerous conjectures arising from Dominic’s work: proved, disproved, and still open. One of the proved ones is featured in the citation for the 2022 Fields Medal awarded to June Huh of Princeton University. I’ve tried to lay out motivations for the open ones having important ramifications——the tribute gives links by which to pursue them.

Our condolences to Bridget, their family, and all who were graced to know Dominic over the years. A memorial service and tea reception afterward will be held at Merton College on June 1, 3:00pm UK time (with livestream).

[added Mathematics Genealogy link to Dominic’s students at top; fixed that Farr’s first section is on discrete probability not matroid theory; photo of me and DJAW enhanced via AI by IA Shohreh Bayat]