Brianchon is fair game
Power Overwhelming 2024-03-14
About five years ago I wrote a blog post warning that I thought it was a bad idea to design math olympiads to be completely untrainable, because I think math olympiads should be about talent development rather than just talent identification, yada yada yada.
So now I want to say the other direction: I also don’t want to design math olympiads so that every problem is 100% required to lie in a fixed, rigid, and arbitrary boundary prescribed by some nonexistent syllabus. From a coach’s perspective, I want to reward “good” studying, and whatever “good” means, I think it should include more than zero flexibility and capacity to deal with slight curveballs.
I was reminded of this because there was a recent contest problem (I won’t say which one to avoid spoilers) that quoted Brianchon’s theorem. Brianchon’s theorem, for those of you that don’t know, states that the diagonals of a circumscribed hexagon are concurrent. It appears as Theorem 9.55 in my textbook, so it’s not too obscure.
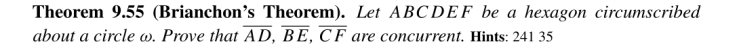
So I was shocked when, after the exam, a number of students complained that this problem was terrible and unfair because it quoted Brianchon’s theorem.
The reason this irked me so much is that there are two other theorems, Pascal’s theorem and La Hire’s theorem (this is a fancy name for pole-polar duality), which are definitely on-syllabus and experienced students are expected to know. Do you know what happens if you put these two together, i.e. if you take the projective dual of Pascal’s theorem?
Yep.
I’m not saying that the whole problem was easy or people should’ve solved it. Actually, the problem’s genuinely tricky and subverts your expectations a bit (as a whole, not just the Brianchon part). I wasn’t too surprised or disappointed by the solve rate on the problem; it was within shouting distance of my prediction.
But I just think “oh, this problem quoted Brianchon” is kind of a lame excuse, because I expect the best students in the country to be able to take the projective dual of Pascal’s theorem.
Or to know that concave functions are minimized at endpoints, as I mentioned a couple years ago for a different problem:
Certainly, there needs to be some informal boundary on exam content, so that the IMO does not degenerate into a trivia contest. However, on the other extreme, I should hope that the world’s best math students are not so inflexible that merely mentioning concavity makes them cower in fear. Change breaks the brittle.