Soma Villanyi: Every d(d+1)-connected graph is globally rigid in d dimensions.
Combinatorics and more 2023-12-31

Today, I want to tell you a little about the following paper that solves a conjecture of Laszlo Lovász and Yechiam Yemini from 1982 and an even stronger conjecture of Bob Connelly, Tibor Jordán, and Walter Whiteley from 2013:
Every  -connected graph is globally rigid in
-connected graph is globally rigid in 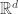 , by Soma Villányi
, by Soma Villányi
Here is the abstract (h/t to Nati Linial for telling me about the paper):
Using a probabilistic method, we prove that
-connected graphs are rigid in
, a conjecture of Lovász and Yemini. Then, using recent results on weakly globally linked pairs, we modify our argument to prove that
-connected graphs are globally rigid, too, a conjecture of Connelly, Jordán and Whiteley. The constant
is best possible.
Let be an abstract graph with
vertices. A
-dimensional framework is an embedding of the vertices of
into
. The embedding is flexible if there is a non-trivial flex, i.e., a non-trivial perturbation of the embedded vertices that keeps all the edge lengths fixed. Here, a trivial flex means a flex that comes from a rigid motion of the entire space. In other words, a trivial flex keeps the distances between every pair of embedded vertices fixed. An embedding is rigid if it is not flexible. There is a related linear notion of infinitesimal flex – an assignment of velocity vectors to the vertices so that the edge length is constant to the first degree. An embedding is globally rigid if every other embedding with the same distances between adjacent vertices is obtained by a rigid motion of
.
A graph G is generically -rigid or simply
-rigid if it is rigid for a generic embedding into
. (This is equivalent to being generically infinitesimally rigid.) A graph is globally
-rigid if it is globaly rigid for a generic embedding into
.
Being -rigid is a mysterious property of graphs and being globally
-rigid is an even more mysterious property. The edges of minimal
-rigid subgraphs of the complete graph on
vertices are the basis of the
-rigidity matroid. A graph is 1-rigid iff it is connected so we can think about
-rigidity as a strong form of connectedness. Another extension of graph connectivity is the notion of
-connected graph, namely a graph that remains connected when we delete every set of at most
vertices. Lovasz and Yemini proved in 1982 that every 6-connected graph is 2-rigid, and made the conjecture that Villanyi has just proved. Jackson and Jordán proved in 2005 that 6-connected graphs are globally 2-rigid.