An attempt to understand the Monster group

The Monster group is very large, very complicated, and very mysterious.

According to the Classification of Finite Simple Groups that was completed last century, the Monster group is the largest of only 26 finite simple groups that do not fit into one of the infinite families of finite simple groups, namely:

• the cyclic groups of prime order;
• the alternating groups on 5 or more objects;
• any of the ‘groups of Lie type‘, which are related to Lie groups but defined over finite fields.

The existence of the Monster was conjectured by Bernd Fischer and later constructed by Robert Griess. This construction was subsequently simplified by John Conway, but the resulting construction is still very complicated and somewhat piecemeal. Both constructions prove that the group is finite by showing that it’s the automorphism group of the Griess algebra defined on the ambient vector space.

Let’s look at the group A5, the smallest of the non-cyclic finite simple groups, by way of analogy. It’s the order-60 group of rotational symmetries of a regular dodecahedron, and this is the lowest-dimensional faithful representation of the group:

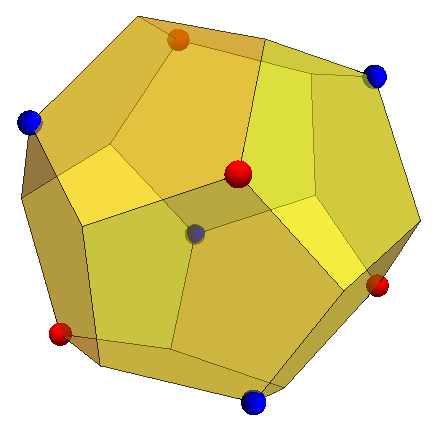
If we choose a coordinate basis for the dodecahedron such that the eight brightly-coloured vertices are (±1, ±1, ±1) and the remaining twelve vertices are the cyclic permutations of (±φ, ±1/φ, 0), then there’s a natural order-12 subgroup generated by cyclic permutations of the vertices together with an even number of sign flips.

This monomial subgroup is also a maximal subgroup, and happens to be the group A4 of rotations fixing a regular tetrahedron, such as the convex hull of the four blue vertices above. We can then describe A5 as being generated from this monomial subgroup together with an ‘exotic element’ ζ that sends:

• (1, -1, -1) → (0, φ, -1/φ);
• (-1, 1, -1) → (φ, -1/φ, 0);
• (-1, -1, 1) → (-1/φ, 0, φ);
• (1, 1, 1) → (-1, -1, -1).

We could also define A5 as the group of rotations which fix the following degree-6 polynomial (x − φy)(y − φz)(z − φx)(x + φy)(y + φz)(z + φx), which is isomorphic to Greg Egan’s potential function discussed here. This is mildly (but not precisely*) analogous to the description of the Monster as the automorphisms of the Griess algebra. Note that the polynomial is clearly invariant under the monomial subgroup A4, and with some effort can be shown to be invariant under the full group A5. Here’s a visualisation of the polynomial:

*in particular, the Griess algebra product and ambient inner product induce a symmetric trilinear real-valued function of three vectors, u.(v × w), whereas the dodecahedral potential is a non-linear real-valued function of a single vector.

Conway’s construction of the Monster group likewise begins with a maximal monomial subgroup, N0 = 2^35 (S3 × M24), and generates the Monster by adding an exotic element. But the construction is much more complicated, because:

• the smallest dimension of a faithful representation of the Monster is 196883, compared with just 3 for the group A5;
• the ambient 196883-dimensional space is a hodgepodge of multiple spaces, constructed in terms of various exceptional objects such as the Leech lattice, Golay code, and Parker loop.

Perhaps we could instead describe the Monster as the group of rotations fixing a set of vertices, in the same way that A5 can be described as the group of rotations fixing the 20 vertices of a dodecahedron? Again, this is possible: there’s a permutation representation on 97239461142009186000 vertices, namely the axes fixed by the centralisers of a certain important conjugacy class of elements in the Monster group (known as ‘transpositions’, ‘type-2A elements’, ‘short involutions’, or ‘Fischer involutions’).

The slight problem is that there are too many such vertices to write down explicitly. But maybe we can utilise the monomial subgroup, in the same way we did for A5: instead of listing all 20 vertices of the dodecahedron, it sufficed to list two of them, namely (1, 1, 1) and (0, φ, -1/φ), since the others are the images of one of these vertices under the action of the monomial subgroup.

Describing lattice points using the monomial subgroup

This same strategy (of describing a monomial subgroup together with a representative of each orbit) has already shown success in terms of studying one of the less complicated exceptional objects, the Leech lattice, where coordinates for the 196560 minimal nonzero vectors can be described efficiently as the set of images of:

• (-3, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1);
• (4, 4, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0);
• (2, 2, 2, 2, 2, 2, 2, 2, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0);

where there are 98304 images of the first vector, 1104 images of the second vector, and 97152 images of the third vector. The monomial subgroup is the full automorphism group 2^12 (M24) of the binary Golay code (viewed as a subset of the vertices of a 24-dimensional cube, {-1, 1}^24) generated by coordinate permutations in M24 together with patterns of sign changes which coincide with elements of the Golay code. The Conway group Co0 is then generated by this monomial subgroup together with an exotic element, as before.

For the 20 vertices of the dodecahedron, we ended up with 2 orbits of points. For the 196560 minimal vectors of the Leech lattice, we have 3 orbits of points. We can ask the concrete question:

How many orbits are there, under the monomial subgroup N0 of the Monster group, of the 97239461142009186000 type-2A axes?

along with the natural follow-up questions:

What are the sizes of the orbits? And can we concisely describe coordinates of representatives of each orbit?

This set of vertices (whose automorphism group is the Monster) might give us more insight into the group, as well as providing a more convenient means of calculating with the group. There’s a Python package by Martin Seysen (from this year!) that could prove useful in trying to answer these questions.

We can also ask whether there’s a nice lattice associated with the Monster group, in the same way that the Leech lattice is associated with the Conway group Co0. There’s an allusion in Conway’s paper to such a lattice being investigated by Simon Norton, but this seemed to be a dead-end: I couldn’t find anything further on the topic, despite asking on MathOverflow.

Fortunately, Richard Borcherds (who won a Fields Medal for proving the monstrous moonshine conjecture) gave a talk on sporadic groups for the Archimedeans, and I was able to ask him about Norton’s lattice.

He responded by mentioning that he recalled that Norton’s lattice didn’t turn out to be unimodular, but that Scott Carnahan had recently constructed a unimodular lattice with Monster group symmetries. Carnahan obtains this lattice (in corollary 3.24) as the weight-2 subspace of an integral form he constructs on the monster vertex operator algebra, an infinite-dimensional graded algebra of which the Griess algebra is the weight-2 subspace.

It would be instructive to translate Carnahan’s lattice into the computationally convenient coordinate system used in Conway’s construction. This would hopefully allow one to study the geometry of the lattice by describing the shells of the lattice as unions of orbits of vectors under the monomial subgroup.