Shallow trees with heavy leaves

There are two very different state-of-the-art chess engines: Stockfish and Leela Chess Zero.

• Stockfish searches many more positions (100 000 000 per second) and evaluates them using computationally cheap heuristics. The tree search methodology is a refinement of alpha-beta pruning.
• Leela Chess Zero, a descendant of DeepMind’s AlphaZero, searches much fewer positions (40 000 per second), using a deep convolutional neural network (trained through millions of games of self-play) to evaluate positions. It has a different search methodology, namely Monte Carlo tree search.

The neural network employed by Leela Chess Zero is itself fascinating, using an architecture similar to the SE-ResNet image classification model. This residual tower of squeeze-and-excitation layers feeds into separate ‘value’ and ‘policy’ heads, for evaluating the position and deciding what to do next, respectively.

However, I want to talk more about the general strategy of searching much fewer positions and expending more effort on each position. In particular, this major difference between Stockfish and Leela Chess Zero is reflected in two of the many search programs used to find spaceships in Conway’s Game of Life and related cellular automata:

• The program ntzfind, originally written by a pseudonymous author ‘zdr’ and enhanced by Matthias Merzenich, Aidan Pierce, and Tom Rokicki, is a depth-first tree search which uses a huge in-memory lookup table to find all possible choices for the next row based on previous rows.
• The new program ikpx2, adapted from the program I wrote to find the first elementary knightship, is more analogous to Leela Chess Zero in that its search tree is much smaller, but the amount of work done at each node is much greater.

In particular, ikpx2 uses a SAT solver to perform a deep lookahead to determine whether the current partial spaceship can be fully extended for several* more rows, and is therefore not close to a ‘dead end’. By comparison, ntzfind can only rule out a partial by performing a depth-first traversal of the entire subtree.

*this is configurable, but a typical value is 30.

The SAT solvers used are Armin Biere’s kissat and CaDiCaL. Kissat is more optimised than CaDiCaL, but doesn’t support incremental solving yet. As such, ikpx2 tries to learn (using basic reinforcement learning, specifically a multi-armed bandit model) which SAT solver is more appropriate for a given task. Theoretically, we could add additional state-of-the-art SAT solvers such as Mate Soos’s cryptominisat, and use a more powerful reinforcement learning model (such as a neural network) to evaluate the subproblem and decide which solver to use.

Having this ‘shallow tree with heavy leaves’ means that the current search progress can easily fit entirely within memory. Also, parallelism is easy: we keep a priority queue of tasks (partial spaceships) and have many CPU threads which do the following:

1. remove a task from the queue;
2. solve it using SAT solvers;
3. communicate the results back to the main orchestrating thread.

The results that are sent back to the main orchestrating thread are partials that have been extended (for 30 or so rows). A small initial segment of those rows are added to the in-memory tree as nodes; the remaining rows are not, as otherwise we’d end up with the same full unpruned search tree used by ntzfind and therefore our advantage is completely annihilated.

What happens to the remaining rows? Instead of merely discarding them, we take the entire extended partial and simulate it in the cellular automaton! Sometimes these partials evolve into an object that the main search couldn’t have found: for example, the tail might have a higher period than the rest of the spaceship, or leave a trail of debris behind. This idea seems to have first been explored by Paul Tooke in 2001, before being rediscovered 20 years later in the context of ikpx2.

Results

One of the early new ikpx2 search results using Paul Tooke’s idea was this partial, which evolves into a period-528 puffer engine:

Similarly, here is a novel period-21 spaceship found by John Winston Garth. He ran ikpx2 to look for 2c/7 spaceships; within 3 days of running on 12 CPU threads, it had both rediscovered David Eppstein’s weekender and found a wholly new period-21 attachment that clings to its tail:

The user ‘iNoMed’ then discovered that two of these could interact to produce an exhaust that can be perturbed by a nearby weekender to emit a forward-moving glider every 42 generations:

Another feature of ikpx2 is its ability to find objects which have different components of different symmetries. Here, for example, is a spaceship with a symmetric head, asymmetric thorax, and symmetric abdomen. The tail is high-period, again having arisen from simulating a partial rather than from direct SAT solving:

Somewhat disappointingly, ikpx2 has not succeeded in finding any new spaceship velocities in the standard Life rules. I tested it on the same input as the original ikpx used to find Sir Robin; ikpx2 was able to find the same result approximately 50x faster (in terms of core-hours elapsed).

There was a recent near-miss, which would be a (2,1)c/7 spaceship were it not for a single extra cell born in generation 7 (the left configuration, with or without the indicated green triplet, gives rise to the right configuration with the frustrating red tetraplet):

The existence of near-misses such as this one makes me hopeful that it will eventually find a (2,1)c/7 spaceship given more time.

Other cellular automata

Unlike the original version of ikpx, this version is able to search a wide family of related cellular automata. In particular, it extracts the set of prime implicants from the cellular automaton rule (regarded as a 9-input 1-output boolean function) and uses that to encode the mechanics of the rule into the SAT problems.

In particular, two invocations of ikpx2 were sufficient to find the following growing knightship in the rule Day&Night: one invocation to find the fast (2,1)c/5 frontend which stretches a thick oblique line, and another invocation to find a slower (2,1)c/6 tail which consumes it:

Here’s an 11c/22 spaceship in a nonstandard rule found by lemon41625, which is an even better demonstration of the symmetry switching. The discovery consists of odd-symmetric, asymmetric, and even-symmetric components with a high-period exhaust:

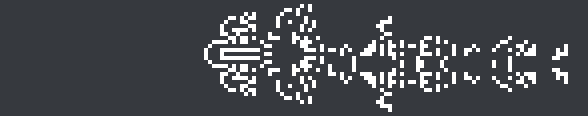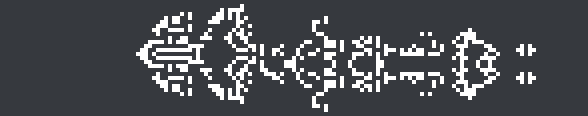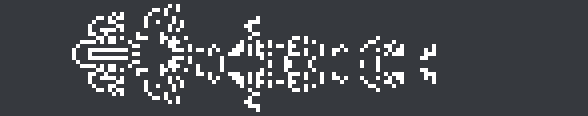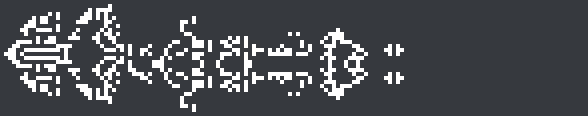
Source code

The source code for ikpx2 is open-source (released under an MIT licence) so you can experiment with it yourself. It’s currently x86_64-specific, because it has apgsearch as a dependency (in order to quickly simulate the partials and examine whether they evolve into anything remotely interesting).