Involutions on a finite set

Suppose that R is the (assumed to be finite) set of solutions to a certain problem, and you’re interested in determining the parity of |R|. The following proof strategy works surprisingly often, namely in at least two different scenarios, and leads to very elegant proofs:

• Embed R in a larger set S equipped with an involution f : S → S, such that R is precisely the set of fixed points of f;
• Define a second involution g : S → S, such that the set T of fixed points of g is easily seen to have the correct parity (usually by having 0 or 1 elements).

Then we have |R| = |S| = |T| (mod 2).

We’ll discuss two examples of this proof technique.

Example I: Zagier’s one-sentence proof

To prove Fermat’s theorem that every prime of the form 4k + 1 is expressible as the sum of two squares, Zagier famously provided the following ‘one-sentence proof’ discussed here:

Here, g is the complicated piecewise involution defined above, and f is the involution which interchanges the second and third coordinates. The set R is the set of ways to write , and the set U is the singleton set containing the fixed point of the complicated involution g.

Observe that this proof is constructive: you can use these involutions f and g to construct a solution to the original problem! Specifically, if you start at the (unique) element of U and alternately apply f and g, the other end of the path is an element of R:

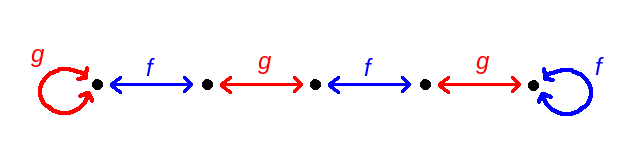
Christian Elsholtz similarly noticed this construction here albeit with the Greek letters α and β to refer to the two involutions.

At first, I though that this was a trick rather than a technique. In the words of Donald Knuth:

A trick is a clever idea that can be used once, while a technique is a mature trick that can be used at least twice.

That was until recently when I saw the following.

Example II: Hamiltonian cycles on cubic graphs

The problem is to show that, given a 3-regular graph G with a distinguished edge x, that there exists an even number of Hamiltonian cycles passing through x. Using this proof approach, we let:

• S be the set of proper 3-edge-colourings (with colours red, green, and blue) of the graph G such that x is assigned the colour blue;
• g be the involution that swaps red and green;
• f be the involution that swaps blue and green on every blue-green component other than the one containing the edge x.

The fixed points of f are those where the green and blue edges form a single (Hamiltonian) cycle. There are no fixed points of g, so U is the empty set. It follows, therefore, that |S| and |R| are also even.

Again, this proof is constructive: by alternately applying f and g, this gives you an explicit self-inverse way to transform any Hamiltonian cycle through x into a different Hamiltonian cycle through x:

This is a natural bijection, in that it doesn’t involve making any arbitrary choices such as labelling the vertices of G. Even better, it’s acceptable for constructivists since we can provide an explicit upper bound on the length of the path of alternating applications of f and g: it’s no longer than the size of S, which is in turn upper-bounded by 3^(3n/2); there are 3n/2 different edges, each of which is either red, green, or blue.

Anyway, does this technique have a name? If not, I’d propose ‘Zagiery’ after the discoverer of the first proof. And are there any other applications besides the two that we’ve looked at?