Agent-Based Models (Part 11)

Last time I began explaining how to run the Game of Life on our software for stochastic C-set rewriting systems. Remember that a stochastic stochastic C-set rewriting system consists of three parts:

• a category C that describes the type of data that’s stochastically evolving in time

• a collection of ‘rewrite rules’ that say how this data is allowed to change

• for each rewrite rule, a ‘timer’ that says the probability that we apply the rule as a function of time.

I explained all this with more mathematical precision in Part 9.

Now let’s return to an example of all this: the Game of Life. To see the code, go here.

Specifying the category C

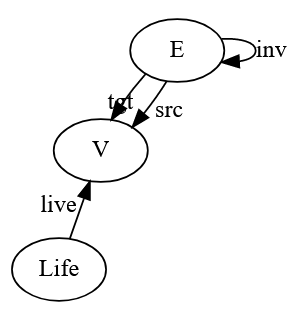
Last time we specified a category C for the Game of Life. This takes just a tiny bit of code:

using AlgebraicABMs, Catlab, AlgebraicRewriting@present SchLifeGraph <: SchSymmetricGraph begin   Life::Ob  live::Hom(Life,V)end

This code actually specifies a ‘schema’ for C, as explained last time, and it calls this schema SchLifeGraph. The schema consists of three objects:

four morphisms:

and three equations:

We can automatically visualize the schema, though this doesn’t show the equations:

An instance of this schema, called a C-set, is a functor F: C → Set. In other words, it’s:

• a set of edges F(E), • a set of vertices F(V), also called cells in the Game of Life • a map F(src): F(E) → F(V) specifying the source of each edge, • a map F(tgt): F(E) → F(V) specifying the target of each edge, • a map F(inv): F(E) → F(E) that turns around each edge, switching its source and target, such that turning around an edge twice gives you the original edge again, • a set F(Life) of living cells, and • a map F(live): F(Life) → F(V) saying which cells are alive.

More precisely, cells in the image of F(Life) are called alive and those not in its image are called dead.

Specifying the rewrite rules and timers

Next we’ll specify 3 rewrite rules for the Game of Life, and their timers. The code looks like this; it’s terse, but it will take some time to explain:

# ## Create model by defining update rules# A cell dies due to underpopulation if it has # < 2 living neighborsunderpop =   TickRule(:Underpop, to_life, id(Cell);   ac=[NAC(living_neighbors(2))]);# A cell dies due to overpopulation if it has # > 3 living neighborsoverpop =   TickRule(:Overpop, to_life, id(Cell);   ac=[PAC(living_neighbors(4))]);# A cell is born if it has 3 living neighborsbirth = TickRule(:Birth, id(Cell), to_life;                  ac=[PAC(living_neighbors(3; alive=false)),                     NAC(living_neighbors(4; alive=false)),                     NAC(to_life)]); 

These are the three rewrite rules:

• underpop says a vertex in our graph switches from being alive to dead if it has less than 2 living neighbors

• overpop says a vertex switches from being alive to dead if it has more than 3 living neighbors

• birth says a vertex switches from being dead to alive if it has exactly 3 living neighbors.

Each of these rewrite rules comes with a timer that says the rule is applied wherever possible at each tick of the clock. This is specified by invoking TickRule, which I’ll explain in more detail elsewhere.

In Part 9 I said a bit about what a ‘rewrite rule’ actually is. I said it’s a diagram of C-sets

where is monic. The idea is roughly that we can take any C-set, find a map from into it, and replace that copy of with a copy of This deserves to be explained more clearly, but right now I just want to point out that in our software, we specify each rewrite rule by giving its morphisms and

For example,

underpop = TickRule(:Underpop, to_life, id(Cell);

says that underpop gives a rule where is a morphism called to_life and is a morphism called id(Cell). to_life is a way of picking out a living cell, and id(Cell) is a way of picking out a dead cell. So, this rewrite rule kills off a living cell. But I will explain this in more detail later.

Similarly,

TickRule(:Overpop, to_life, id(Cell);

kills off a living cell, and

birth = TickRule(:Birth, id(Cell), to_life;

makes a dead cell become alive.

But there’s more in the description of each of these rewrite rules, starting with a thing called ac. This stands for application conditions. To give our models more expressivity, we can require that some conditions hold for each rewrite rule to be applied! This goes beyond the framework described in Part 9.

Namely: we can impose positive application conditions, saying that certain patterns must be present for a rewrite rule to be applied. We can also impose negative application conditions, saying that some patterns must not be present. We denote the former by PAC and the latter by NAC. You can see both in our Game of Life example:

# ## Create model by defining update rules# A cell dies due to underpopulation if it has # < 2 living neighborsunderpop =   TickRule(:Underpop, to_life, id(Cell);   ac=[NAC(living_neighbors(2))]);# A cell dies due to overpopulation if it has # > 3 living neighborsoverpop =   TickRule(:Overpop, to_life, id(Cell);   ac=[PAC(living_neighbors(4))]);# A cell is born if it has 3 living neighborsbirth = TickRule(:Birth, id(Cell), to_life;                  ac=[PAC(living_neighbors(3; alive=false)),                     NAC(living_neighbors(4; alive=false)),                     NAC(to_life)]); 

For underpop, the negative application condition says we cannot kill off a cell if it has 2 distinct living neighbors (or more).

For overpop, the positive application condition says we can only kill off a cell if it has 4 distinct living neighbors (or more).

For birth, the positive application condition says we can only bring a cell to life if it has 3 distinct living neighbors (or more), and the negative application conditions say we cannot bring it to life it has 4 distinct living neighbors (or more) or if it is already alive.

There’s a lot more to explain. Don’t be shy about asking questions! But I’ll stop here for now, because I’ve shown you the core aspects of Kris Brown’s code that expresses the Game of Life as a stochastic C-set writing system.