Home Online Mathematical Communication Azimuth Stirling’s Formula from Statistical Mechanics

Stirling’s Formula from Statistical Mechanics

Azimuth 2024-08-28

Physicists like to study all sorts of simplified situations, but here’s one I haven’t seen them discuss. I call it an ‘energy particle’. It’s an imaginary thing with no qualities except energy, which can be any number \ge 0.

I hate it when on Star Trek someone says “I’m detecting an energy field” — as if energy could exist without any specific form. That makes no sense! Yet here I am, talking about energy particles.

Earlier on the n-Café, I once outlined a simple proof of Stirling’s formula using Laplace’s method. When I started thinking about statistical mechanics, I got interested in an alternative proof using the Central Limit Theorem, mentioned in a comment by Mark Meckes. Now I want to dramatize that proof using energy particles.

The basic idea

Stirling’s formula says

\displaystyle{ n! \sim \sqrt{2 \pi n} \, \left(\frac{n}{e}\right)^n }

where \sim means that the ratio of the two quantities goes to 1 as n \to \infty. Some proofs start with the observation that

\displaystyle{ n! = \int_0^\infty x^n \, e^{-x} \, d x }

This says that n! is the Laplace transform of the function x^n. Laplace transforms are important statistical mechanics. So what is this particular Laplace transform, and Stirling’s formula, telling us about statistical mechanics?

It turns out this Laplace transform shows up naturally when you consider a collection of energy particles!

Statistical mechanics says that at temperature T, the probability for an energy particle to have energy E follows an exponential distribution: at temperature T it’s proportional to \exp(-E/k T) where k is Boltzmann’s constant. From this you can show the expected energy of this particle is k T, and the standard deviation of its energy is also k T.

Next suppose you have n energy particles at temperature T, not interacting with each other. Each one acts as above and they’re all independent. As n \to \infty, you can use the Central Limit Theorem to show the probability distribution of their total energy approaches a Gaussian with mean n k T and standard deviation \sqrt{n} k T. But you can also compute the probability distribution exactly from first principles, and you get an explicit formula for it. Comparing this to the Gaussian, you get Stirling’s formula!

In particular, the \sqrt{2 \pi} that you see in a Gaussian gives the \sqrt{2 \pi} in Stirling’s formula.

The math behind this argument is here, without any talk of physics:

• Aditya Ghosh, A probabilistic proof of Stirling’s formula.

The only problem is that it contains a bunch of rather dry calculations. If we use energy particles, these calculations have a physical meaning!

The downside to using energy particles is that you need to know some physics. So let me teach you that. If you know statistical mechanics well, you can probably skip this next section. If you don’t, it’s probably more important than anything else I’ll tell you today.

Classical statistical mechanics

When we combine classical mechanics with probability theory, we can use it to understand concepts like temperature and heat. This subject is called classical statistical mechanics. Here’s how I start explaining it to mathematicians.

A classical statistical mechanical system is a measure space (X,\mu) equipped with a measurable function

H : X \to [0,\infty)

We call X the state space, call points in X the states of our system, and call H its Hamiltonian: this assigns a nonnegative number called the energy H(x) to any state x \in X.

When our system is in thermal equilibrium at temperature T we can ask: what’s the probability of the system’s state x being in some subset of X? To answer this question we need a probability measure on X. We’ve already got a measure d\mu(x), but Boltzmann told us the chance of a system being in a state of energy E is proportional to

e^{- \beta E}

where \beta = 1/k T, with T being temperature and k being a physical constant called Boltzmann’s constant. So we should multiply d\mu(x) by e^{-\beta H(x)}. But then we need to normalize the result to get a probability measure. We get this:

\displaystyle{ \frac{ e^{-\beta H(x)} \; d\mu(x) }{ \int_X e^{-\beta H(x)} \; d\mu(x) } }

This is the so-called Gibbs measure. The normalization factor on bottom is called the partition function

Z(\beta) = \displaystyle{ \int_X e^{-\beta H(x)} \; d\mu(x) }

and it winds up being very important. (I’ll assume the integral here converges, though it doesn’t always.)

In this setup we can figure out the probability distribution of energies that our system has at any temperature. I’ll just tell you the answer. For this it’s good to let

\nu(E) = \mu(\{x \in X \vert \; H(x) \le E \}

be the measure of the set of states with energy \le E. Very often

d\nu(E) = g(E) \, d E

for some integrable function g \colon \mathbb{R} \to \mathbb{R}. In other words,

g(E) = \frac{d \nu(E)}{d E}

where the expression at right is called a Radon–Nikodym derivative. Physicists call g the density of states because if we integrate it over some interval (E, E + \Delta E] we get ‘the number of states’ in that energy range. That’s how they say it, anyway. What we actually get is the measure of the set

\{x \in X: \; E < H(x) \le E + \Delta E \}

We can express the partition function in terms of g, and we get this:

Z(\beta) = \int_0^\infty e^{-\beta E} \, g(E) \; d E

So we say the partition function is the Laplace transform of the density of states.

We can also figure out the probability distribution of energies that our system has at any temperature, as promised. We get this function of E:

\displaystyle{ \frac{e^{-\beta E} \, g(E)}{Z(\beta)} }

This should make intuitive sense: we take the density of states and multiply it by e^{-\beta E} following Boltzmann’s idea that the probability for the system to be in a state of energy E decreases exponentially with E in this way. To get a probability distribution, we then normalize this.

An energy particle

Now let’s apply statistical mechanics to a very simple system that I haven’t seen physicists discuss.

An energy particle is a hypothetical thing that only has energy, whose energy can be any nonnegative real number. So it’s the classical statistical mechanical system whose measure space is ([0,\infty), dx), and whose Hamiltonian is the identity function:

H(E) = E

We can answer some questions about energy particles using the stuff I explained in the last section:

1) What’s the density of states of an energy particle? It’s just 1.

2) What’s the partition function of an energy particle? It’s

\int_0^\infty e^{-\beta E} \; d E = \frac{1}{\beta}

3) What’s the probability distribution of energies of an energy particle? It’s the exponential distribution

\frac{1}{\beta} e^{-\beta E}

4) What’s the mean energy of an energy particle? It’s the mean of the above probability distribution, which is

\frac{1}{\beta} = k T

5) What’s the variance of the energy of an energy particle? It’s

\frac{1}{\beta^2} = (k T)^2

Nice! We’re in math heaven here, where everything is simple and beautiful. We completely understand a single energy particle.

But I really want to understand a finite collection of energy particles. Luckily, there’s a symmetric monoidal category of classical statistical mechanical systems, so we can just tensor a bunch of individual energy particles. Whoops, that sounds like category theory! We wouldn’t want that — physicists might get scared. Let me try again.

The next section is well-known stuff, but also much more important than anything about ‘energy particles’.

Combining classical statistical mechanical systems

There’s standard way to combine two classical statistical mechanical systems and get a new one. To do this, we take the product of their underlying measure spaces and add their Hamiltonians. More precisely, suppose our systems are (X,\mu,H) and (X', \mu', H'). Then we form the product space X \times X', give it the product measure \mu \otimes \mu', and define the Hamiltonian

H \otimes H' \colon X \times X' \to [0,\infty)

by

(H \otimes H')(x,x') = H(x) + H'(x')

We get a new system (X \times X', \mu \otimes \mu', H \otimes H').

When we combine systems in this way, a lot of nice things happen:

1) The density of states for the combined system is obtained by convolving the densities of states for the two separate systems.

2) The partition function of the combined system is the product of the partition functions of the two separate systems.

3) At any temperature, the probability distribution of energies of the combined system is obtained by convolving those of the two separate systems.

4) At any temperature, the mean energy of the combined system is the sum of the mean energies of the two separate systems.

5) At any temperature, the variance in energy of the combined system is the sum of the variances in energies of the two separate systems.

The last three of these follow from standard ideas on probability theory. For each value of \beta, the rules of statistical mechanics give this probability measure on the state space of the combined system:

\displaystyle{ \frac{ e^{-\beta (H(x) + H'(x'))} \; d\mu(x) \otimes d\mu'(x') }{ \int_{X \times X'} e^{-\beta (H(x) + H'(x'))} \; d\mu(x) d\mu'(x')} }

But this is a product measure: it’s clearly the same as

\displaystyle{ \frac{ e^{-\beta H(x)} \; d\mu(x) }{ \int_{X} e^{-\beta (H(x)} \; d\mu(x) } \otimes \frac{ e^{-\beta H'(x')} \; d\mu(x) }{ \int_{X'} e^{-\beta (H'(x')} \; d\mu'(x') } }

Thus, in the language of probability theory, the energies of the two systems being combined are independent random variables. Whenever this happens, we convolve their probability distributions to get the probability distribution of their sum. The mean of their sum is the sum of their means. And the variance of their sum is the sum of their variances!

It’s also easy to see why the partition functions multiply. This just says

\displaystyle{ \int_{X \times X'} e^{-\beta (H(x) + H'(x'))} \; d\mu(x) d\mu'(x') =} \displaystyle{ \left(\int_{X} e^{-\beta (H(x)} \; d\mu(x) \right) \left(\int_{X'} e^{-\beta (H'(x')} \; d\mu'(x') \right) }

Finally, since the partition functions multiply, and the partition function is the Laplace transform of the density of states, the densities of states must convolve: the Laplace transform sends convolution to multiplication.

A system of n energy particles

You can iterate the above arguments to understand what happens when you combine any number of classical statistical mechanical systems. For a system of n energy particles the state space is [0,\infty)^n, with Lebesgue measure as its measure. The energy is the sum of all their individual energies, so it’s

H(E_1, \dots, E_n) = E_1 + \cdots + E_n

Let’s work out the density of states g. We could do this by convolution but I prefer to do it from scratch — it amounts to the same thing. The measure of the set of states with energy \le E is

\nu(E) = \mu(\{x \in [0,\infty)^n \vert \; H(x) \le E \}

This is just the Lebesgue measure of the simplex

\{ (E_1, \dots, E_n) \vert \; E_i \ge 0 \; \text{and} \; E_1 + \cdots + E_n \le E \}

I hope you’re visualizing this simplex, for example when n = 3:

                                 

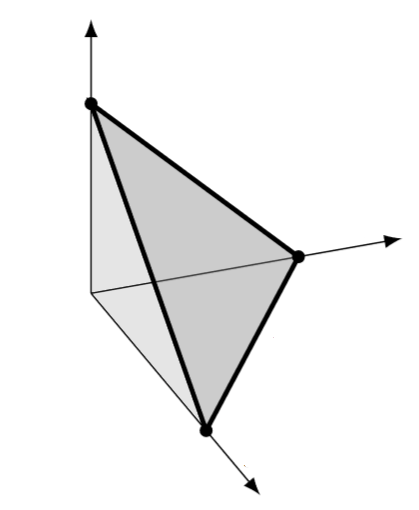
Its volume is well known to be 1/n! times that of the hypercube [0,E]^n:

\nu(E) = \frac{E^n}{n!}

Differentiating this we get the density of states:

g(E) = \frac{d\nu(E)}{d E} = \frac{E^{n-1}}{(n-1)!}

So, the partition function of a collection of $n$ energy particles is

\int_0^\infty e^{-\beta E} \; g(E) \; d E = \int_0^\infty e^{-\beta E} \; \frac{E^{n-1}}{(n-1)!} \; d E = \frac{1}{\beta^n}

In the last step I might have done the integral, or I might have used the fact that we already know the answer.

You may wonder why we’re getting these factors of (n-1)! when studying n energy particles. If If you think about it, you’ll see why. The density of states is the derivative of the volume of this n-simplex as a function of E:

                                 

But that’s the area of the (n-1)-simplex shown in darker gray, which is E^{n-1}/(n-1)!.

Now we know everything we want:

1) What’s the density of states of n energy particles? It’s

\frac{E^{n-1}}{(n-1)!}

2) What’s the partition function of n energy particles? It’s

\frac{1}{\beta^n}

3) What’s the probability distribution of energies of an energy particle? It’s the so-called gamma distribution

\frac{1}{\beta^n} \, e^{-\beta E} \, \frac{E^{n-1}}{(n-1)!}

4) What’s the mean total energy of n energy particles? It’s

\frac{n}{\beta} = n k T

5) What’s the variance of the total energy of n energy particles? It’s

\frac{n}{\beta^2} = n (k T)^2

Now that we’re adding independent and identically distributed random variables, you can tell we are getting close to the Central Limit Theorem, which says that a sum of a bunch of those approaches a Gaussian — at least when each one has finite mean and variance, as holds here.

Stirling’s formula

What is the probability distribution of energies of a system made of n energy particles? We’ve used statistical mechanics to show that it’s

\displaystyle{ \frac{1}{\beta^n} \, e^{-\beta E} \, \frac{E^{n-1}}{(n-1)!} }

But the energy of each particle has mean 1/\beta and variance 1/\beta^2, and these energies are independent random variables. So the Central Limit Theorem says their sum is asymptotic to a Gaussian with mean n/\beta and variance n/\beta^2, namely

\displaystyle{ \frac{1}{\sqrt{2 \pi n /\beta^2}} e^{(E - n/\beta)^2/(2 n / \beta^2)} }

We obtain a complicated-looking asymptotic formula:

\displaystyle{ \frac{1}{\beta^n} \, e^{-\beta E} \, \frac{E^{n-1}}{(n-1)!} \; \sim \; \frac{1}{\sqrt{2 \pi n /\beta^2}} e^{(E - n/\beta)^2/(2 n / \beta^2)} }

But if we simplify this by taking \beta = 1, we get

\displaystyle{ e^{- E} \, \frac{E^{n-1}}{(n-1)!} \sim \frac{1}{\sqrt{2 \pi n}} e^{(E - n)^2/2 n} }

and if we then take E = n, we get

\displaystyle{ e^{-n} \, \frac{n^{n-1}}{(n-1)!} \sim \frac{1}{\sqrt{2 \pi n}} }

Fiddling around a bit we get Stirling’s formula:

\displaystyle{ n! \sim \sqrt{2 \pi n} \, \left(\frac{n}{e}\right)^n }

Unfortunately this argument isn’t rigorous yet: I’m acting like the Central Limit Theorem implies pointwise convergence of probability distributions to a Gaussian, but it’s not that strong. So we need to work a bit harder. For the details I leave you to Aditya Ghosh’s article.

But my goal here was not really to dot every i and cross every t. It was to show that Stirling’s formula emerges naturally from applying standard ideas in statistical mechanics and the Central Limit Theorem to large collections of identical systems of a particularly simple sort.