Polarities (Part 1)
Azimuth 2024-11-03
This is a progress report on some joint work with Xiaoyan Li, Nathaniel Osgood and Evan Patterson. Together with collaborators we have been developing software for ‘system dynamics’ modelling, and applying it to epidemiology—though it has many other uses. We’ve written two papers about it, and given plenty of talks:
• Software for compositional modeling.
But the software keeps growing—so it’s time to write another paper or two! First we’re writing one aimed at applied category theorists, where we explain the math in detail, and don’t pull any punches. One small part of this paper involves the concept of ‘polarities’. Let me explain those now.
Causal loop diagrams
In the tradition of system dynamics we model systems at various levels of detail using at least three kinds of diagrams. The most detail is provided by stock and flow diagrams: from such a diagram we can recover a system of first-order ordinary differential equations describing how quantities called ‘stocks’ change due to ‘flows’ between these stocks. A ‘system structure diagram’ is like a stock and flow diagram without the functions describing how flows are functions of stocks. The least detail is provided by a causal loop diagram, and this is what I want to talk about now.
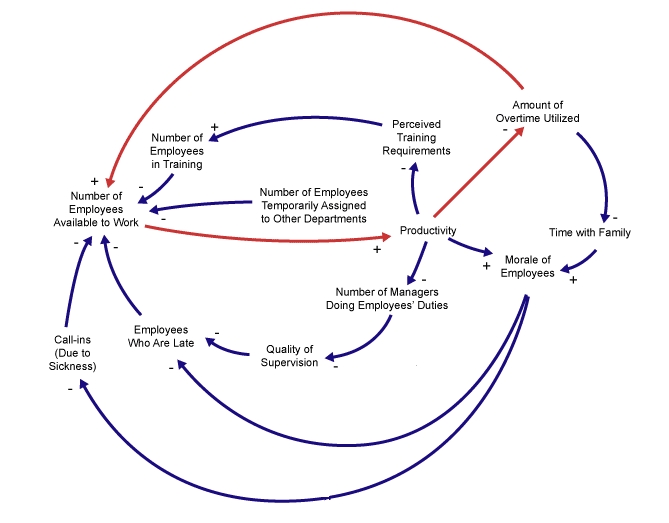
Here is a causal loop diagram drawn by Six Sigma, a consulting company that aims to help you find problems in your organization and fix them:
Mathematically a causal loop diagram is a graph whose edges are labeled by signs, + and -. A positive edge
means that increasing tends to increase
while decreasing
tends to decrease
A negative edge
means that increasing tends to decrease
while decreasing
tends to increase
As the name suggests, the main use of causal loop diagrams is to detect feedback loops. Suppose we go around a loop of edges, multiplying the signs as we go, following the usual rules:
If the result is a + sign, then we call this loop a positive feedback loop. If the result is a – sign, we call this loop a negative feedback loop.
For example, here is a positive feedback loop:
Increasing the number of employees available to work increases productivity, which decreases the number of managers doing employees’ duties, which increases the quality of supervision, which decreases the employees who are late, which increases the number of employees available to work!
Can you spot a negative feedback loop in this diagram?
Polarities
So far all this is very simple—and indeed that’s part of the point: causal loop diagrams are so easy to understand that you can walk into a business, talk to them about their problems, and start drawing diagrams that shed light on the feedback loops that they’re encountering.
But causal loop diagrams get a bit more interesting when we replace signs by more general ‘polarities’. Mathematically, polarities can be elements of any monoid: a set with an associative multiplication and a unit element. The monoid of signs, , is better known to mathematicians as the abelian group
But there’s no need for polarities to form a group, and there’s no need for the multiplication to be commutative. In principle any monoid will work, though some simple ones seem to be the most useful.
For example we can take our set of polarities to be
where 0 means ‘indeterminate’. Now this edge:
means that increasing the quantity could either increase or decrease quantity
and similarly decreasing
could have either effect. We can multiply these polarities as we did before, with the additional rule that 0 times anything equals 0.
Mathematicians will instantly recognize that this multiplication rule makes the set into a monoid. It happens to be isomorphic to the multiplicative monoid of the ring
The multiplicative group of
meaning the group of elements that have multiplicative inverses, is the smaller monoid
we saw earlier.
There are other interesting monoids we can use as polarities. But instead of listing a bunch, let me explain a simple thing what we do wit causal loop diagrams. It’s something we’ve already been talking about.
From causal loop diagrams to categories
Let’s be a bit more formal. A graph with edges and vertices
is a pair of functions
We say is the source of the edge
and
is its target.
Given any set we can label the edges of
by elements of
To do this we just pick a function
But when the set is a monoid, we can do more! In this case let’s call the whole setup
a causal loop diagram over I don’t really like this term—it will be confusing to mathematicians—but it’s appropriate for work in the field of system dynamics, so let’s use it just for now.
What can we do with a causal loop diagram over We can form the free category
on our graph, and get a way to label morphisms in this category by elements of
A morphism in the category
is just an edge path in
i.e. a list of edges
where the target of each edge is the source of the next. So, it makes sense to label
by the element
defined using multiplication in the monoid
For example, suppose is the two-element monoid
latex f$ is the red loop here, saying starting and ending at ‘amount of overtime utilized’, it will get labeled by -.
This means it’s a negative feedback loop.
But what’s really going on here? We have a map that sends morphisms in
to elements of
but it’s better than just an arbitrary map of sets, because it obeys
So, this map is really a functor from to some category! Which category? It’s called the delooping
of the monoid
It has just one object
and a morphism
for each element
Composition of morphisms in this category is just multiplication in
Note, we don’t need to say what our functor
does to objects, since has just one object
All that matters is what
does to morphisms, and we’ve specified that.
This viewpoint is quite nice. For example, the ‘free’ functor
has a right adjoint
sending any category to its underlying graph. Using the properties of adjoints, our functor
gives a map of graphs
Here is the graph with one vertex $\star$ and one edge for each element of
A map of graphs
simply labels every edge of
with an element of
So, it’s only a slight abuse of language to call this map of graphs
It’s just our original labeling dressed up in fancy categorical clothes. And while we’re dressing up and formalizing things, we can summarize our observation as an official Lemma:
Lemma. Given a monoid and a graph
labelings of the edges of
by elements of
correspond bijectively to functors
since is left adjoint to
There’s a lot more to say, but I’ll stop here for now and continue later. I’ve decided people just don’t read long blog articles.