Polarities (Part 2)

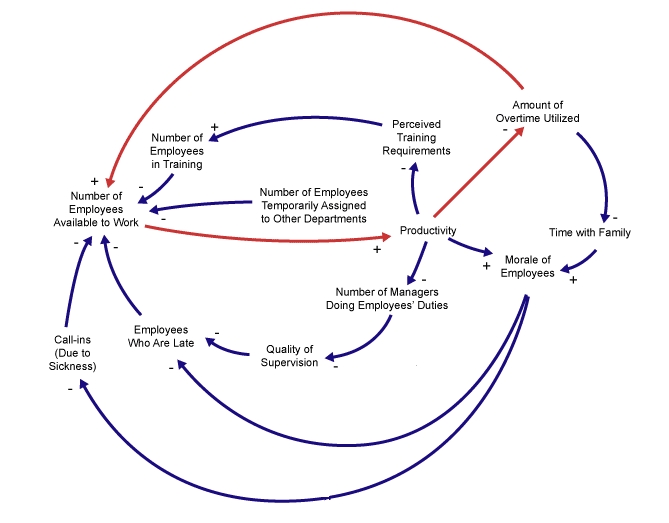
Last time I explained ‘causal loop diagrams’, which are graphs with edges labeled by plus or minus signs, or more general ‘polarities’. These are a way to express qualitatively, rather than quantitatively, how entities affect one another.

For example, here’s how causal loop diagrams us say that alcoholism ‘tends to increase’ domestic violence:

We don’t need to specify any numbers, or even need to say what we mean by ‘tends to increase’, though this leads to the danger of using the term in a very loose way.

You may wonder what’s the point. One point is that causal loop diagrams are often used as a first step toward building more quantitative models. Another is that people can learn about feedback loops they may not have noticed, simply by drawing a causal loop diagram of a situation and searching for loops in it. Many people do this. For example, the consulting company Six Sigma will do it for your business:

This is pretty cool. As a mathematician, I don’t want to limit myself to the quantitative: I can’t resist making up mathematical theories of the qualitative. So together with my coauthors—Xiaoyan Li, Nathaniel Osgood and Evan Patterson—I’ve been exploring the math of causal loop diagrams.

Today, after a quick review, I want to explain three ways to get new causal loop diagrams from old:

• change of monoid • pulling back along a map of graphs • pulling forward along a map of graphs

The third is by far the most subtle and interesting. It requires working with something more sophisticated than a mere monoid of polarities. I’ll explain.

Quick review

A graph is a set of edges, a set of vertices, and two functions

assigning to each edge its source and target. A causal loop diagram over a monoid is a graph as above together with a map

sending each edge of the graph to an element of which we call the label of that edge. We call the monoid of polarities.

The category of causal loop diagrams

This isn’t quite a review, but I should have mentioned it last time. Whenever you have some sort of mathematical gadget it’s your duty to define the category of such gadgets.

There’s a category of causal loop diagrams over a fixed monoid In fact this category is very nice: it’s an example of what we call a topos. But for now, I’ll just explain in a down-to-earth way what a morphism of causal loop diagrams is!

Suppose we have two causal loop diagrams over say

and

What’s a morphism from the first to the second? It’s just a pair of functions

that get along with sources, targets and labelings:

To compose morphisms, we just compose their functions between edges and compose their functions between vertices.

Change of monoid

As I said, there are various ways to get new causal loop diagrams from old. For example, we might want to change our minds about what monoid we’re using for polarities. This is really easy if we have a homomorphism of monoids

Then we can take any casual loop diagram over

and turn it into a causal loop diagram over

You can check that this process gives a functor from the category of causal loop diagrams over to the category of causal loop diagrams over

Example. For example, we might want to take a causal loop diagram over the monoid of signs , and think of it as a special case of a causal loop diagram over the larger monoid which includes the ‘indeterminate’ sign We can do this using the obvious inclusion of monoids

Example. There is also an interesting homomorphism of monoids

from the multiplicative monoid of real numbers to sending all the positive numbers to all the negative numbers to and zero to This lets turn a causal loop diagram with ‘quantitative’ information about how much each vertex affect each other into one with merely ‘qualitative’ information.

Yes, the world of the qualitative and the world of the quantitative are not separate worlds! We have a kind of ‘forgetful’ functor from the quantitative to the qualitative, sending any graph with edges labeled by real numbers to the same graph with edges labeled by and

Pulling back along a map of graphs

Suppose we have a map of graphs from

to

Suppose the second graph has a labeling making it a causal loop diagram over some monoid

Then we can ‘pull back’ this labeling and make the first graph into a causal loop diagram over

How? Well, a map of graphs is a pair of functions

obeying a couple of equations:

So, we can make our first graph into a causal loop diagram with the labeling

That’s all there is to it! Our map of graphs then automatically becomes a morphism of causal loop diagrams.

Pushing forward along a map of graphs

This is more tricky and interesting. Suppose as before we have a map of graphs from

to

But now suppose the first graph has a labeling making it a causal loop diagram over some monoid

Can we use this to make the second graph into a causal loop diagram over

It’s not obvious how, because we are given a labeling

and a map

and from this we want to get a labeling

There’s no way to do this unless we can pull some trick like take all the edges that map to some edge sum up their labels, and take the resulting sum to be the labeling If only finitely many edges map to and our monoid is commutative, we can actually do this summation using the monoid operation of (If infinitely many edges map to , we get an infinite sum, which is probably bad. And if the monoid is noncommutative, the sum will be ambiguous, since we don’t know in what order to sum the monoid elements.)

This trick is on the right track. But if you look at examples, you’ll see it’s ridiculous to use the monoid operation of to do this sum—and not just because we called this operation ‘multiplication’ rather than ‘addition’.

For example in the monoid of signs, , we have

This says that if a vertex affects a vertex negatively, and affects another vertex negatively, then indirectly affects positively. We saw examples last time:

But now we’re talking about something else: not composing effects, but adding them up. For example, suppose our first graph has two edges from to both labeled with minus signs. That means affects negatively in two different ways. Suppose that these two edges (and no others) get mapped to a single edge in our second graph. Then intuitively, that edge should also describe a negative effect. We should not multiply the two minus signs and get a plus sign! Instead, we should add two negative signs and get another minus sign!

All this suggests that now we want to have a second operation called ‘addition’, in addition to the first one, which we’ve been calling multiplication. This suggests that should be a ring or at the very least a rig (which snobs call a ‘semiring’). The addition is a rig is commutative by definition, so that’s good.

In fact this works nicely. I’ll define a causal loop diagram over a rig to be a causal loop diagram over the underlying multiplicative monoid of that rig. The following lemma is immediate:

Lemma. Suppose is a rig and suppose we are given a causal loop diagram over

Suppose we are given a map of graphs from to a second graph and suppose at most finitely many edges of map to each edge of Then this second graph becomes a causal loop diagram over

where is defined as follows:

where is the map on edges coming from our map of graphs.

What’s next?

This is nice, and we could develop more results about these processes of ‘pulling back’ and ‘pushing forward’ edge labelings along maps of graphs. But before diving into this, it’s good to consider examples, and think about why we actually care about these processes—from the viewpoint of system dynamics, that is.

And when we do that, I believe we’re led into the world of hyperfields. A ‘hyperfield’ is like a field, but where addition and subtraction are multivalued. These are currently quite fashionable in algebraic geometry—admittedly limited quarters of algebraic geometry, but limited quarters that include eminent figures such as Alain Connes and Caterina Consani, who have been using them to think about the Riemann Hypothesis. But I’m interested in them for humbler reasons.

Consider our example Multiplication of signs is easy and obvious:

Division of signs is also easy, which is why I’m talking about fields—or more precisely, hyperfields.

But what should addition be? It seems reasonable that adding and should give and adding and should give But what happens when we add and In other words, if affects positively in one way, and negatively in another, what’s the total effect?

We can’t say whether the total effect positive or negative. It could go either way! But this is what hyperfields were born for: they let addition be multivalued. Thus we define the sum of and to be the set

Next time I want to explain hyperfields, and switch from using rings to using these. But I also need to explain why they’re so interesting for system dynamics.