Star-Autonomous Envelopes
Azimuth 2020-04-21
In the fourth talk of the ACT@UCR seminar, Michael Shulman will tell us how to create nice string diagams for any closed symmetric monoidal category.
His talk will take place on Wednesday April 22nd at 5 pm UTC, which is 10 am in California, or 1 pm on the east coast of the United States, or 6 pm in England. It will be held online via Zoom, here:
https://ucr.zoom.us/j/607160601
Mike has to teach right after his talk, but he will rejoin us for discussions at 8 pm UTC, or 1 pm in California, or 4 pm on the east coast of the US, or 9 pm in England, at the the Category Theory Community Server. You can join those discussion here if you become a member:
• April 22, Michael Shulman, Star-autonomous envelopes.
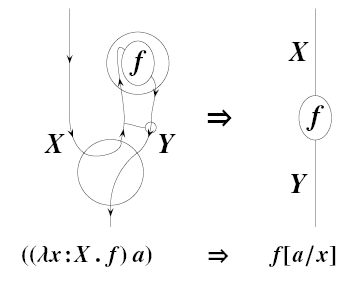
Abstract. Symmetric monoidal categories with duals, a.k.a. compact monoidal categories, have a pleasing string diagram calculus. In particular, any compact monoidal category is closed with [A,B] = (A* ⊗ B), and the transpose of A ⊗ B → C to A → [B,C] is represented by simply bending a string. Unfortunately, a closed symmetric monoidal category cannot even be embedded fully-faithfully into a compact one unless it is traced; and while string diagram calculi for closed monoidal categories have been proposed, they are more complicated, e.g. with “clasps” and “bubbles”. In this talk we obtain a string diagram calculus for closed symmetric monoidal categories that looks almost like the compact case, by fully embedding any such category in a star-autonomous one (via a functor that preserves the closed structure) and using the known string diagram calculus for star-autonomous categories. No knowledge of star-autonomous categories will be assumed.
This is especially interesting to me since Mike Stay and I introduced string diagrams for closed monoidal categories in a somewhat ad hoc way in our Rosetta Stone paper—but the resulting diagrams required clasps and bubbles:
This is the string diagram for beta reduction in the cartesian closed category coming from the lambda calculus.