Maxwell’s Relations (Part 1)

Azimuth 2021-09-18

The Maxwell relations are equations that show up whenever we have a finite-dimensional vector space $V$ and a smooth convex function

$U \colon V \to \mathbb{R}$

They say that the mixed partial derivatives of $U$ commute, but also that the mixed partial derivatives of various functions constructed from $U$ commute. So in a sense they are completely trivial except for the way we construct these various functions! Nonetheless they are very important in physics, because they give generally valid relations between the derivatives of thermodynamically interesting quantities.

For example, here is one of the Maxwell relations that people often use when studying a thermodynamic system like a cylinder of gas or a beaker of liquid:

$\displaystyle{ \left. \frac{\partial T}{\partial V} \right|_S \; = \; - \left. \frac{\partial P}{\partial S} \right|_V }$

where:

• $S$ is the entropy of the system • $T$ is its temperature • $V$ is its volume • $P$ is its pressure

There are also three more Maxwell relations involving these quantities. They all have the same general look, though half contain minus signs and half don’t. So, they’re quite tiresome to memorize. It’s more interesting to figure out what’s really going on here!

I already gave one story about what’s going on: we start with a function $U$ , which happens in this case to be a function of $S$ and $V$ called the internal energy of our system. If we say its mixed partial derivatives commute:

$\displaystyle{ \frac{\partial^2 U}{\partial V \partial S} = \frac{\partial^2 U}{\partial S \partial V} }$

we get the Maxwell relation I wrote above, simply by using the standard definitions of $T$ and $P$ as partial derivatives of $U.$ We can then build a bunch of other functions from $U, S, T, V$ and $P,$ and write down other equations saying that the mixed partial derivatives of these functions commute. This gives us all the Maxwell relations.

Let me show you in detail how this works, but without explaining why I’m choosing the particular ‘bunch of other functions’ that I’ll use. There is a way to explain that using the concept of Legendre transform. But next time I’ll give a very different approach to the Maxwell relations, based on this paper:

• David J. Ritchie, A simple method for deriving Maxwell’s relations, American Journal of Physics 36 (1958), 760–760.

This sidesteps the whole business of choosing a ‘bunch of other functions’, and I think it’s very nice.

What follows is a bit mind-numbing, so let me tell you what to pay attention to. I’ll do the same general sort of calculation four times, first starting with any convex smooth function $U \colon \mathbb{R}^2 \to \mathbb{R}$ and then with three other functions built from that one. The only clever part is how we choose those other functions.

The first relation

We start with any smooth convex function $U$ of two real variables $S, V$ and write its differential as follows:

$dU = T dS - P d V$

This says

$\displaystyle{ T = \left.\frac{\partial U}{\partial S} \right|_V \qquad P = - \left. \frac{\partial U}{\partial V} \right|_S }$

These are the usual definitions of the temperature $T$ and pressure $P$ in terms of the internal energy $U,$ but you don’t need to know anything about those concepts to follow all the calculations to come. In particular, from the pure mathematical viewpoint the minus sign is merely a stupid convention.

The commuting of mixed partials implies

$\displaystyle{ \left. \frac{\partial T}{\partial V} \right|_S \; = \; \left. \frac{\partial}{\partial V} \right|_S \left. \frac{\partial }{\partial S} \right|_V U \; = \; \left. \frac{\partial }{\partial S} \right|_V \left. \frac{\partial}{\partial V} \right|_S U \; = \; - \left. \frac{\partial P}{\partial S} \right|_V }$

giving the first of the Maxwell relations:

$\boxed{ \displaystyle{ \left. \frac{\partial T}{\partial V} \right|_S \; = \; - \left. \frac{\partial P}{\partial S} \right|_V } }$

The second relation

Next, let’s define the Helmholtz free energy

$F = U - TS$

Taking its differential we get

$\begin{array}{ccl} dF &=& dU - d(TS) \\ \\ &=& (T dS - P dV) - (SdT + TdS) \\ \\ &=& - S dT - P d V \end{array}$

so if we think of $F$ as a function of $T, V$ we get

$\displaystyle{ S = - \left.\frac{\partial F}{\partial T} \right|_V \qquad P = - \left. \frac{\partial F}{\partial V} \right|_T }$

The commuting of mixed partials implies

$\displaystyle{ \left. - \frac{\partial S}{\partial V} \right|_T \; = \; \left. \frac{\partial}{\partial V} \right|_T \left. \frac{\partial }{\partial T} \right|_V F \; = \; \left. \frac{\partial }{\partial T} \right|_V \left. \frac{\partial}{\partial V} \right|_T F \; = \; - \left. \frac{\partial P}{\partial T} \right|_V }$

giving the second of the Maxwell relations:

$\boxed{ \displaystyle{ \left. \frac{\partial S}{\partial V} \right|_T \; = \; \left. \frac{\partial P}{\partial T} \right|_V } }$

The third relation

Copying what we did to get the second relation, let’s define the enthalpy

$H = U + P V$

Taking its differential we get

$\begin{array}{ccl} dH &=& dU + d(PV) \\ \\ &=& (T dS - P dV) + (VdP + P dV) \\ \\ &=& T dS + V dP \end{array}$

so if we think of $H$ as a function of $S, P$ we get

$\displaystyle{ T = \left.\frac{\partial H}{\partial S} \right|_P \qquad V = \left. \frac{\partial H}{\partial P} \right|_S }$

The commuting of mixed partials implies

$\displaystyle{ \left. \frac{\partial T}{\partial P} \right|_S \; = \; \left. \frac{\partial}{\partial P} \right|_S \left. \frac{\partial }{\partial S} \right|_P H \; = \; \left. \frac{\partial }{\partial S} \right|_P \left. \frac{\partial}{\partial P} \right|_S H \; = \; \left. \frac{\partial V}{\partial S} \right|_P }$

giving the third of the Maxwell relations:

$\boxed{ \displaystyle{ \left. \frac{\partial T}{\partial P} \right|_S \; = \; \left. \frac{\partial V}{\partial S} \right|_P }}$

The fourth relation

Combining the last two tricks, let’s define the Gibbs free energy

$G = U + PV - TS$

Taking its differential we get

$\begin{array}{ccl} dG &=& dU + d(PV) - d(TS) \\ \\ &=& (T dS - P dV) + (VdP + P dV) - (SdT + TdS) \\ \\ &=& V d P - S dT \end{array}$

so if we think of $G$ as a function of $P, T$ we get

$\displaystyle{ V = \left.\frac{\partial G}{\partial P} \right|_T \qquad S = -\left. \frac{\partial G}{\partial T} \right|_P }$

The commuting of mixed partials implies

$\displaystyle{ \left. \frac{\partial V}{\partial T} \right|_P \; = \; \left. \frac{\partial}{\partial T} \right|_P \left. \frac{\partial }{\partial P} \right|_T G \; = \; \left. \frac{\partial }{\partial P} \right|_T \left. \frac{\partial}{\partial T} \right|_P G \; = \; - \left. \frac{\partial S}{\partial P} \right|_T }$

giving the fourth and final Maxwell relation:

$\boxed{ \displaystyle{ \left. \frac{\partial V}{\partial T} \right|_P \; = \; - \left. \frac{\partial S}{\partial P} \right|_T }}$

Conclusions

I hope you’re a bit unsatisfied, for two main reasons.

The first question you should have is this: why did we chose these four functions to work with:

$U, \; U - ST, \; U + PV, \; U - ST + PV$

The pattern of signs is not really significant here: if we hadn’t followed tradition and stuck a minus sign in our definition of $P$ here:

$\displaystyle{ T = \left.\frac{\partial U}{\partial S} \right|_V \qquad P = - \left. \frac{\partial U}{\partial V} \right|_S }$

everything would look more systematic, and we’d use these four functions:

$U, \; U - ST, \; U - PV, \; U - ST - PV$

This would make it easier to guess how everything works if instead of a function $U \colon \mathbb{R}^2 \to \mathbb{R}$ we started with a function $U \colon \mathbb{R}^n \to \mathbb{R}.$ We could write this as

$U(q^1, \dots, q^n)$

and define a bunch of functions

$\displaystyle{ p_i = \frac{\partial U}{\partial q^i} }$

called ‘conjugate quantities’.

Then, we could get $2^n$ different functions by starting with $U$ and subtracting off products of the form $p_i q^i$ where $i$ ranges over some subset of $\{1, \dots, n\}.$

Then we could take mixed partial derivatives of these functions, note that the mixed partial derivatives commute, and get a bunch of Maxwell relations — maybe

$\displaystyle{ 2^n \frac{n(n-1)}{2} }$

of them! (Sanity check: when $n$ is 2 this is indeed 4.)

The second question you should have is: how did I sneakily switch from thinking of $U$ as a function of $S$ and $V$ to thinking of $F$ as a function of $T$ and $V,$ and so on? How could I get away with this? I believe the answer to this involves the concept of Legendre transform, which works well when $U$ is convex.

Answering these questions well might get us into a bit of contact geometry. That would be nice. But instead of answering these questions next time, I’ll talk about Ritchie’s approach to deriving Maxwell’s equations, which seems to sidestep the two questions I just raised!

Just for fun

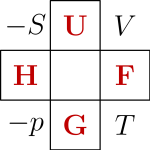
Finally: students of thermodynamics are often forced to memorize the Maxwell relations. They sometimes use the thermodynamic square:

where for some idiotic reason the $p$ for pressure is written lower-case—perhaps so you can mix it up with momentum!

If you like puzzles, maybe you can figure out how the thermodynamic square works if you stare at it along with the four Maxwell equations I derived:

$\displaystyle{ \left. \frac{\partial T}{\partial V} \right|_S \; \phantom{-} = \; - \left. \frac{\partial P}{\partial S} \right|_V }$

$\displaystyle{ \left. \frac{\partial S}{\partial V} \right|_T \; \phantom{-} = \; \phantom{-} \left. \frac{\partial P}{\partial T} \right|_V }$

$\displaystyle{ \left. \frac{\partial T}{\partial P} \right|_S \; \phantom{-} = \; \phantom{-} \left. \frac{\partial V}{\partial S} \right|_P }$

$\displaystyle{ \left. \frac{\partial V}{\partial T} \right|_P \; \phantom{-} = \; - \left. \frac{\partial S}{\partial P} \right|_T }$

Again, it probably be easier if we hadn’t stuck a minus sign into the definition of pressure. If you get stuck, click on the link.

Unfortunately the thermodynamic square is itself so hard to memorize that students resort to a mnemonic for that! Sometimes they say “Good Physicists Have Studied Under Very Fine Teachers” which gives the letters “GPHSUVFT” that you see as you go around the square.

I will never try to remember any of these mnemonics. But I wonder if there’s something deeper going on here. So:

Puzzle. How does the thermodynamic square generalize if $U$ is a function of 3 variables instead of 2? How about more variables?

For more on Maxwell’s relations and how they’re connected to Hamilton’s equations, see this post of mine:

• Classical mechanics versus thermodynamics.