Zipf's demon
Language Log 2024-10-25
George Kingsley Zipf is famous for his work on the power-law distribution of word frequencies, which has come to be known as Zipf's Law. And he's also known for the related "Law of Abbreviation", and the hypothesized balance between effort and efficacy.
In his 1945 paper "The repetition of words, time-perspective, and semantic balance", Zipf looks at a different distribution, which is much less famous:
In the present study we shall attempt to show in preliminary outline how the rate of repetition of words in the stream of speech may be useful not only in indicating what we shall presently define as "time-perspective" but also in elucidating what we shall presently refer to as "semantic balance" – two terms of potential significance in the understanding of personality variants.
"Personality variants?" Wait for it…
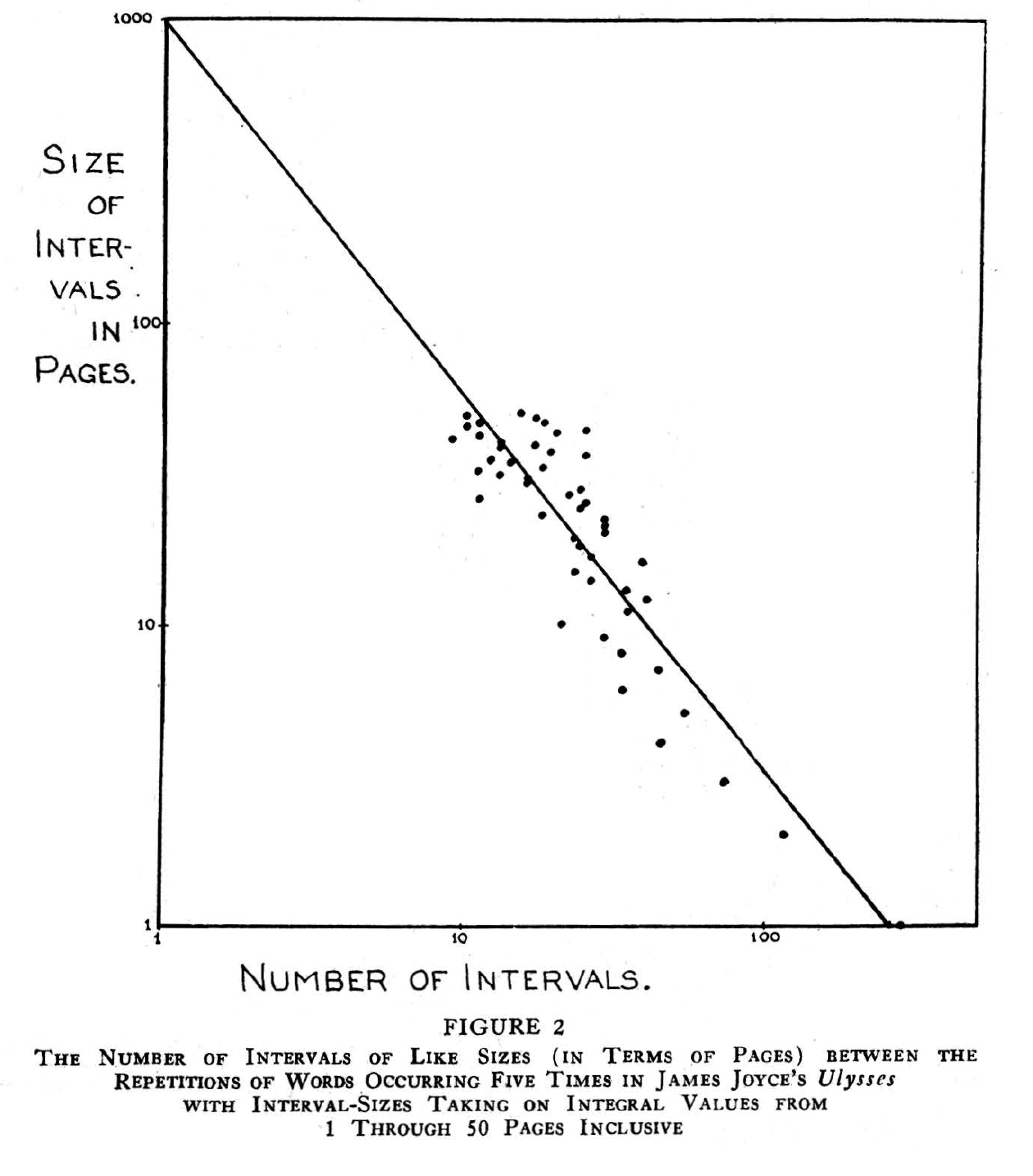
That paper's Figure 2, which presents its main empirical evidence about word-repetition intervals, gives us a clue about why the initial uptake for this idea was so slow:
Caption: The Number of Intervals of Like Sizes (in Terms of Pages) between the Repeitions of Words Occurring Five Times in James Joyce's Ulysses with Interval-Sizes Taking on Integral Values from 1 Through 50 Pages Inclusive.
Zipf could start from published word-count data in that case — M.L. Hanley's 1937 Word Index to James Joyce's Ulysses — but the analysis was still a labor-intensive addition to Hanley's labor-intensive foundation. Digital text and computer analysis make such analyses easy today, by comparison, though few have done it. More on that in a later post.
For now, I want to share with you a striking (or maybe weird) idea that occupies most of Zipf's 1945 paper, presenting a mathematical model for a demon ringing a set of bells.
Zipf introduces his bell-demon this way:
Let us take n bells that are equivalent in size and equally difficult to ring, and then let us attach them to a long straight board in such a manner that the bells are equally spaced along the board. At one end of the board we shall place a blackboard ruled with n-columns for the respective bells; and we shall also station a demon there to act as bell-ringer. The demon must ring one bell once each second of .time, and after he has finished ringing a bell once he must return to the blackboard to record that fact in the bell's column. Thus in order to ring one bell 10 times, or 10 bells once each, he will make 10 round trips down the board and back in the space of 10 seconds, and will have 10 marks therefor on the blackboard. (And we shall ask the demon to make his round trips over shortest distances).
This analogue is interesting for many reasons. First of all the demon's work, w, in terms of making a round trip to ring a given bell, will increase in direct proportion to the bell's distance, d, from the blackboard (or w = d). And since the distance of the respective bells increases integrally from the blackboard (i.e., ld, 2d, 3d, ….., nd), it follows that the bells are arranged in respect of the the demon's work, w, in getting to and from them according to the simple series, lw, 2w, 3w, ….. , nw . .
Now if we ask our demon to ring each bell with a frequency, f, that is inversely proportionate to the round-trip work involved, or in equation form, $w X f = C$, he will ring the closer (and easier) bells proportionately more often than the distant (and harder) bells. And since the ranked-frequency in decreasing order, r, with which each bell is rung will be equal to the bell's w above, we come upon the familiar equation:
(1) $r X f = C$
However if we now ask the demon to ring all bells according to Equation 1 but to stop after he has rung the nth and farthest bell once (n = C) and after he has rung all other bells their allotted times, then the n bells will have been rung approximately according to the equation
$$F \cdot Sn = \frac{F}{1} +\frac{F}{1} + \frac{F}{2}+ \frac{F}{3} + . . . . . +\frac{F}{n}$$
in which $F\cdot Sn$ represents the total of round trips made (as well as the total number of running seconds of time) and where $F$ represents the total number of times the nearest bell is rung, and where $\frac{F}{n} = 1$ (or, if you will, where $F = n$), with p omitted above because it equals 1.
This gives him his power law for the counts of individual bells, but so far, it puts no constraint on their inter-ringing intervals. As he observes:
Of course the above equation puts no restriction upon the order in which the demon rings the bells. Thus he may ring the nearest bell its allotted $F$ times before ringing the 2nd nearest bell its allotted $F / 2$ times, and so on progressively down the board until he has rung the nth and farthest bell a single time. In short he might always ring "the easiest remaining bell first," while postponing as long as possible the more distant and. hence more difficult bells. The chief drawback of ringing "the easiest first" is that the demon will be forced to run faster and faster, and therefore to work at an ever increasing rate, as he proceeds farther and farther down the board, if he is to complete each round-trip within the prescribed second. And in so doing he will be unevenly distributing his work over time with the risk of collapsing before he gets the nth bell rung.
So he adds a policy to optimize the demon's effort:
In order to correct this uneven distribution of work over time, we may ask the demon to distribute his work as evenly as possible over time while still ringing his bells according to Equation 3. Yet as soon as he does distribute his work evenly over time, he will automatically ring the bells in such a way that the sizes of the interval, $I_{f}$, between the respective repetitions of the bells will approximate the equation:
(4) $N^{p} \cdot I_{f} =$ a constant
with the exponent, $p$, equal to 1.
For more demonic mathematics about "balancing the frequency of easy acts against the rarity of difficult acts", read the paper, if you're interested. For present purposes, let's jump to Zipf's observation about the "abnormal time-perspective […] represented by the median 1.20 slope of Joyce's Ulysses […] which suggests a slightly abnormal preference for longer intervals".
Thus having once "rung a bell," Joyce tends systematically to avoid its repetition abnormally. In other words, events of the past (as represented by words) seem to be systematically more remote from the present than is actually the case with 1.00 time-perspective. Although this general type of over-long time distortion is probably not infrequent among those personalities who focus their attention primarily upon the present moment, it is interesting to note that this particular distortion of time is found in a novel that is characterized for just that attribute (if we may so interpret the words, "stream of consciousness" writing).
And now the punch line:
Other types of time-perspective — and not necessarily linear — can be defined in terms of the bell-analogy, yet there is one we mention cursorily lest it be ignored. we refer to the case in which the demon saves work and simplifies the problem of distributing his work evenly over time by simply bending the straight board into a quasi-arc. In this fashion the distant bells become nearer, and the demon can take short-cuts to them. This type of time-distortion we shall call schizophrenic unbalance and we shall treat it in greater detail in a future publication.
Time-perspective, in terms of the distribution of minimalized work over time (with all its endless ramifications) would seem to be an inviting topic for the study of the normal and abnormal of human mental behavior.
As far as I can tell, Zipf never actually treated "schizophrenic unbalance […] in greater detail in a future publication". This may be because he died in 1950 at the age of 48.
Nor did anyone else follow up on inter-word repetition statistics as a sign of "schizophrenic unbalance", at least not using the same phrase — though their are some adjacent things, like this paper, and commenters may be able to point us to others.
Update — To avoid further misunderstandings, let me point out that the cited 2013 paper (Todder et al., "Non-Linear Dynamic Analysis of Inter-Word Time Intervals in Psychotic Speech") is based on a completely different measure.
Zipf's metric was the interval (in pages) between two occurrences of the same word, e.g. the word "accurate" occurs in Ulysses on pages 434, 575, 590, 605, and 615, yielding intervals of 141, 15, 15, and 10 pages.
Todder et al. measure the interval in seconds between successive words (whatever they are) in the stream of speech, so that the production in TIMIT of SA1 by speaker FLNH0
0.188 0.378 she0.378 0.637 had0.587 0.703 your0.703 1.010 dark1.010 1.339 suit1.339 1.426 in1.426 1.773 greasy1.773 2.091 wash2.149 2.478 water2.478 2.643 all2.643 2.938 year
yields inter-word-onset intervals in seconds of
0.190 0.209 0.116 0.307 0.329 0.087 0.347 0.376 0.329 0.165