How many unique English tweets are possible? How long would it take for the population of the world to read them all out loud?

—Eric H., Hopatcong, NJ

High up in the North in the land called Svithjod, there stands a rock. It is a hundred miles high and a hundred miles wide. Once every thousand years a little bird comes to this rock to sharpen its beak. When the rock has thus been worn away, then a single day of eternity will have gone by.

—Hendrik Willem Van Loon

Tweets are 140 characters long. There are 26 letters in English—27 if you include spaces. Using that alphabet, there are \( 27^{140} \approx 10^{200} \) possible strings.

But Twitter doesn't limit you to those characters. You have all of Unicode to play with, which has room for over a million different characters. The way Twitter counts Unicode characters is complicated, but the number of possible strings could be as high as \( 10^{800} \).

Of course, almost all of them would be meaningless jumbles of characters from a dozen different languages. Even if you're limited to the 26 English letters, the strings would be full of meaningless jumbles like "ptikobj". Eric's question was about tweets that actually say something in English. How many of those are possible?

This is a tough question. Your first impulse might be to allow only English words. Then you could further restrict it to grammatically valid sentences.

But it gets tricky. For example, “Hi, I’m Mxyztplk” is a grammatically valid sentence if your name happens to be Mxyztplk. (Come to think of it, it’s just as grammatically valid if you’re lying.) Clearly, it doesn’t make sense to count every string that starts with “Hi, I’m ...” as a separate sentence. To a normal English speaker, “Hi, I’m Mxyztplk” is basically indistinguishable from “Hi, I’m Mxzkqklt”, and shouldn't both count. But “Hi, I’m xPoKeFaNx” is definitely recognizably different from the first two, even though “xPoKeFaNx” isn’t an English word by any stretch of the imagination.

Fortunately, there’s a better approach.

Let’s imagine a language which has only two valid sentences, and every tweet must be one of the two sentences. They are:

1. “There’s a horse in aisle five.”
2. “My house is full of traps.”

Twitter would look like this:

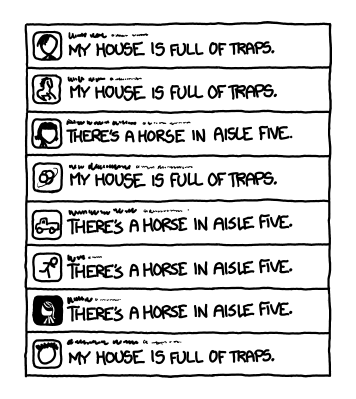
The messages are relatively long, but there’s not a lot of information in each one—all they tell you is whether the person decided to send the trap message or the horse message. It’s a 1 or a 0. Although there are a lot of letters, for a reader who knows the pattern the language carries only one bit of information per sentence.

This example hints at a very deep idea, which is that information is fundamentally tied to the recipient’s uncertainty about the message’s content and their ability to predict it in advance.

Claude Shannon—who almost singlehandedly invented modern information theory—had a clever method for measuring the information content of a language. He showed groups of people samples of typical written English which were cut off at a random point, then asked them to guess which letter came next.

Based on the rates of correct guesses—and rigorous mathematical analysis—Shannon determined that the information content of typical written English was around 1.0 to 1.2 bits per letter. This means that a good compression algorithm should be able to compress ASCII English text—which is eight bits per letter—to about 1/8th of its original size. Indeed, if you use a good file compressor on a .txt ebook, that’s about what you’ll find.

If a piece of text contains n bits of information, in a sense it means that there are \( 2^n \) different messages it can convey. There’s a bit of mathematical juggling here (involving, among other things, the length of the message and the concept of unicity distance), but the bottom line is that it suggests there are on the order of about \( 2^{140\times1.1} \approx 2\times10^{46} \) meaningfully different English tweets, rather than \( 10^{200} \) or \( 10^{800} \).

Now, how long would it take the world to read them all out?

Reading \( 2\times10^{46} \) tweets would take a person nearly \( 10^{47} \) seconds. It’s such a