It’s martingale time, baby! How to evaluate probabilistic forecasts before the event happens? Rajiv Sethi has an idea. (Hint: it involves time series.)

My Columbia econ colleague writes:

The following figure shows how the likelihood of victory for the two major party candidates has evolved since August 6—the day after Kamala Harris officially secured the nomination of her party—according to three statistical models (Trump in red, Harris in blue):

Market-derived probabilities have fluctuated within a narrower band. The following figure shows prices for contracts that pay a dollar if Harris wins the election, and nothing otherwise, based on data from two prediction markets (prices have been adjusted slightly to facilitate interpretation as probabilities, and vertical axes matched to those of the models):

So, as things stand, we have five different answers to the same question—the likelihood that Harris will prevail ranges from 51 to 60 percent across these sources. On some days the range of disagreement has been twice as great.

As we’ve discussed, a difference in 10% of predicted probability corresponds to roughly a difference of 0.4% (that is, 0.004) in predicted vote share. So, yeah, it makes complete sense to me that different serious forecasts would differ by this much, also it makes sense that markets could be different by this much. (As Rajiv discussed in an earlier post, for logistical reasons it’s not easy to arbitrage between the two markets shown above, so it’s possible for them to maintain some daylight between them.)

Also, this is a minor thing but if you’re gonna plot two lines that add to a constant, it’s enough to just plot one of them. I say this in part out of general principles and in part because these lines that cross 0.5 create shapes and other visual artifacts such as the “vase” in PredictIt plot. I think these visual artifacts get in the way of seeing and learning from the data.

OK, that’s all background. Different forecasts differ. The usual way we talk about evaluating forecast is by comparing to outcomes. Rajiv writes:

The standard approach would involve waiting until the outcome is revealed and then computing a measure of error such as the average daily Brier score. This can and will be done, not just for the winner of the presidency but also the outcomes in each competitive state, the popular vote winner, and various electoral college scenarios.

I think the evaluation should be done on vote margin, not on the binary win/loss outcome, as the evaluation based on a binary outcome is hopelessly noisy, a point that’s come up on this blog many times and which I explained again last month. Even if you use the vote margin, though, you still have just one election outcome, and that won’t be enough for you to compare different reasonable forecasts.

Rajiv has a new idea:

But there is a method of obtaining a tentative measure of forecasting performance even prior to event realization. The basic idea is this. Imagine a trader who believes a particular model and trades on one of the markets on the basis of this belief. Such a trader will buy and sell contracts when either the model forecast or the market price changes, and will hold a position that will be larger in magnitude when the difference between the forecast and the price is itself larger. This trading activity will result in an evolving portfolio with rebalancing after each model update. One can look at the value of the resulting portfolio on any given day, compute the cumulative profit or loss over time, and use the rate of return as a measure of forecasting accuracy to date.

This can be done for any model-market pair, and even for pairs of models or pairs of markets (by interpreting a forecast as a price or vice versa).

I don’t agree with everything Rajiv does here—he writes, “The trader was endowed with $1,000 and no contracts at the outset, and assigned preferences over terminal wealth given by log utility (to allow for some degree of risk aversion),” which makes no sense to me, as I think anyone putting $1000 in a prediction market would be able to lose it all without feeling much bite—but I’m guessing that if the analysis were switched to a more sensible linear utility model, the basic results wouldn’t change.

Rajiv summarizes his empirical results:

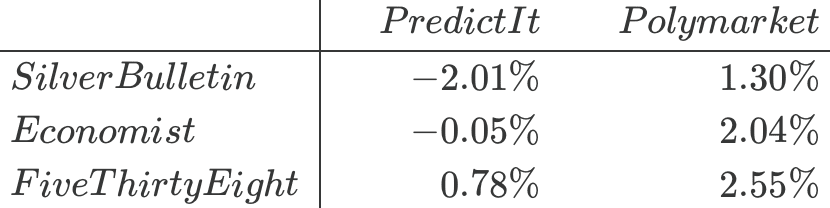
Repeating this exercise for each model-market pair, we obtain the following returns:

Among the models, FiveThirtyEight performs best and Silver Bulletin worst against each of the two markets, though the differences are not large. And among markets, PredictIt is harder to beat than Polymarket.

I don’t take this as being a useful evaluation of the three public forecasts, because . . . these are small numbers, and this is still just N = 1. It’s one campaign we’re talking about. Another way to put it is: What are the standard errors on these numbers? You can’t get a standard error from only one data point.

This doesn’t mean that the idea is empty; we should just avoid overinterpreting the results.

I haven’t fully processed Rajiv’s idea but I think it’s connected to the martingale property of coherent probabilistic forecasts, as we’ve discussed in the context of betting on college basketball and elections.

However you look at it, the thing that will kill your time series of forecasts is too much volatility: if you anticipate having to incorporate a flow of noisy information, you need to anchor your forecasts (using a “prior” or a “model”) to stop your forecast from being bounced around by noise.

Unfortunately, that goal of sensible calibrated stability runs counter to another goal of public forecasters, which is to get attention! For that, you want your forecast to jump around so that you are continuing to supply news.

I sent the above to Rajiv, who wrote:

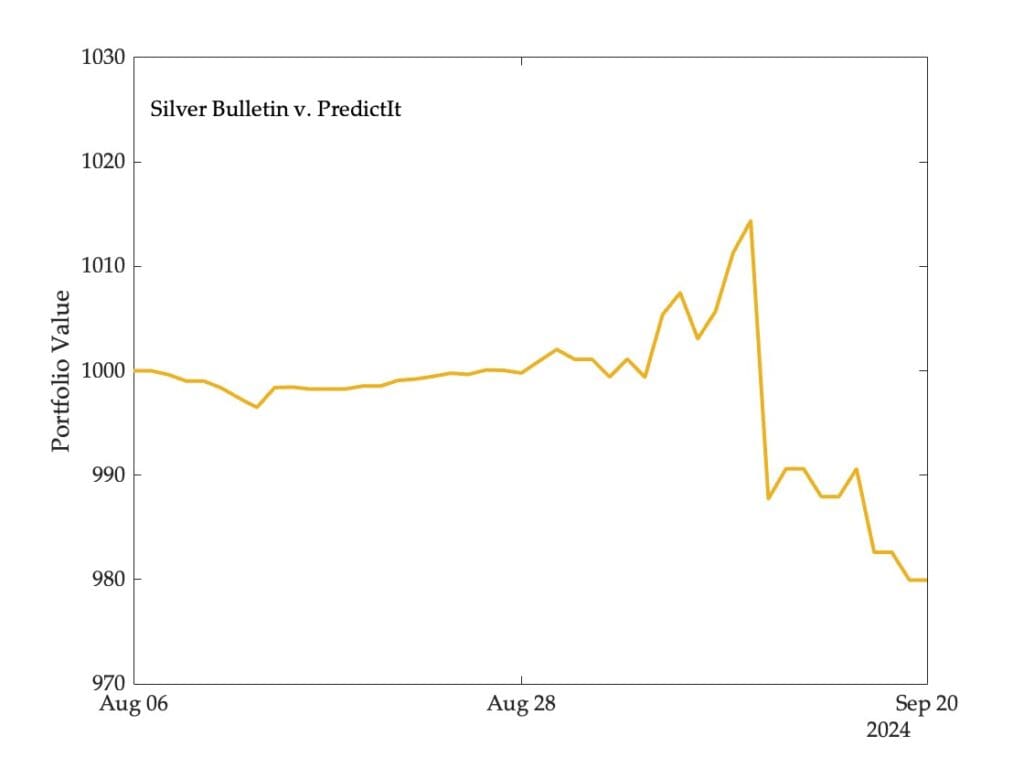
One thing I didn’t show in the post is the how the value of the portfolio (trading on PredictIt) would have evolved over time:

You will see that if I had conducted this analysis a couple of weeks ago, Silver Bulletin would have been doing well. It really suffered when the price of the Harris contract rose on the markets, since it was holding a significant short position.

The lesson here (I think) is that we need lots of events to come to any conclusion. I am working on the state level and popular vote winner forecasts, but of course these will all be correlated so doesn’t really help much with the problem of small numbers of events. This is the Grimmer-Knox-Westwood point as I understand it.

If we were to apply this sort of procedure retroactively to past time series of forecasts or betting markets that were too variable because they were chasing the polls too much, then I’d think/hope it could reveal the problems. After 2016, forecasters have worked hard to keep lots of uncertainty in their forecasts, and I think that one result of that is to keep the market prices more stable.