Supporting Bayesian modeling workflows with iterative filtering for multiverse analysis

Anna Riha, Nikolas Siccha, Antti Oulasvirta, and Aki Vehtari write:

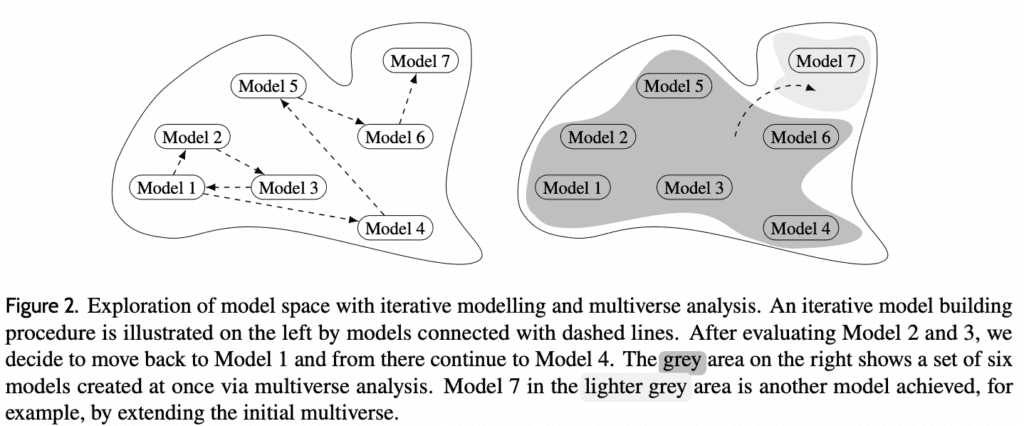
When building statistical models for Bayesian data analysis tasks, required and optional iterative adjustments and different modelling choices can give rise to numerous candidate models. In particular, checks and evaluations throughout the modelling process can motivate changes to an existing model or the consideration of alternative models to ultimately obtain models of sufficient quality for the problem at hand. Additionally, failing to consider alternative models can lead to overconfidence in the predictive or inferential ability of a chosen model. The search for suitable models requires modellers to work with multiple models without jeopardising the validity of their results. Multiverse analysis offers a framework for transparent creation of multiple models at once based on different sensible modelling choices, but the number of candidate models arising in the combination of iterations and possible modelling choices can become overwhelming in practice. Motivated by these challenges, this work proposes iterative filtering for multiverse analysis to support efficient and consistent assessment of multiple models and meaningful filtering towards fewer models of higher quality across different modelling contexts. Given that causal constraints have been taken into account, we show how multiverse analysis can be combined with recommendations from established Bayesian modelling workflows to identify promising candidate models by assessing predictive abilities and, if needed, tending to computational issues. We illustrate our suggested approach in different realistic modelling scenarios using real data examples.

They’re just getting started! Lots more needs to be done. I’ve been interested in the general idea for awhile; the challenge is to get it working for some good examples and then to develop more general tools and abstract more general principles. As Riha et al. demonstrate, it can help to work in the directions of modeling and computation at the same time.