Average predictive comparisons

A political science colleague asked me what I thought of this recent article by Carlisle Rainey, which begins:

Some work in political methodology recommends that applied researchers obtain point estimates of quantities of interest by simulating model coefficients, transforming these simulated coefficients into simulated quantities of interest, and then averaging the simulated quantities of interest . . . But other work advises applied researchers to directly transform coefficient estimates to estimate quantities of interest. I point out that these two approaches are not interchangeable and examine their properties. I show that the simulation approach compounds the transformation-induced bias . . .

By quantities of interest, he’s referring to summaries such as “predicted probabilities, expected counts, marginal effects, and first differences.”

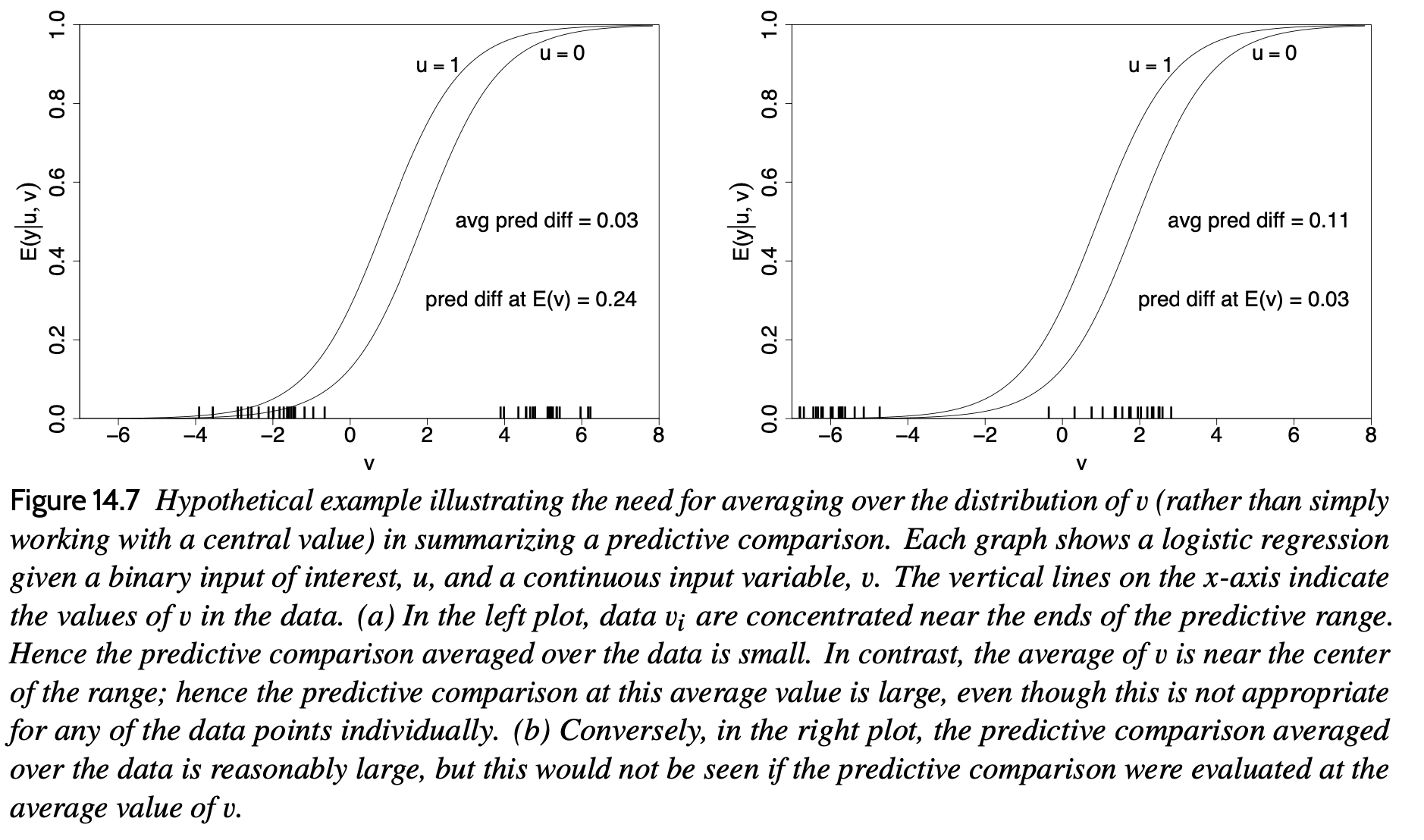
Statistical theory is focused on the estimation of parameters in a model, not so much on inference for derived quantities, and it turns out that these questions are subtle. There are no easy answers, as Iain Pardoe and I realized years ago when trying to come up with general rules for estimating average predictive comparisons.

Here’s how we put it in Section 14.4 of Regression and Other Stories:

It’s a fun problem, typical of many math problems in that there’s no way to talk about the correct answer until you decide what’s the question! The predictive comparison—sometimes we call it the average predictive effect of u on y, other times we avoid the term “effect” because of its implication of causality—depends on the values chosen for u^lo and u^hi, it depends on the values of the other predictors v, and it depends on the parameter vector theta. For a linear model with no interactions, all these dependences go away, but in general the average predictive comparison depends on all these things.

So, along with evaluating different estimators of the average predictive comparison (or other nonlinear summaries such as predicted probabilities and expected counts), we need to decide what we want to be estimating. And that’s no easy question!

For more on the topic, I recommend my 2007 paper with Pardoe, Average predictive comparisons for models with nonlinearity, interactions, and variance components.

The topic has confused people before; see for example here.

I think the problem arises because of a mistaken intuition that there should be a single correct answer to this question. The issues that Rainey discusses in his article are real, and they arise within a larger context of trying to provide methods for researchers who are producing inferential summaries without always having a clear sense of what they are trying to estimate. I’m not slamming these researchers—it’s not always clear to me what summaries I’m interested in.

Again, I recommend our 2007 paper. Many open questions remain!