New paper on conformal prediction and human decisions

This is Jessica. I’ve previously written some posts musing about conformal prediction as a decision aid. Part of what got me interested in it as a method for quantifying uncertainty is the tension between how on the one hand, prediction sets might seem more intuitive or concrete to decision makers (compared to providing a pseudo-probability that a prediction is correct like a softmax value), but on the other hand, it’s unclear what the typical decision-theoretic utility-maximizing agent would do with a conformal prediction set. Now I’ve written a paper reflecting on this further. 

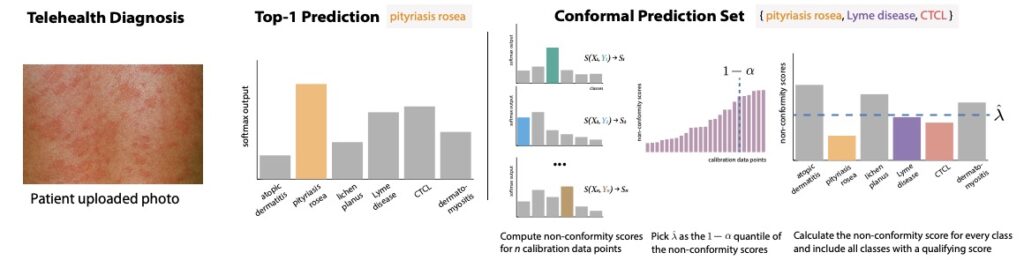
As a brief reminder of what conformal prediction is, in a classification setting, split conformal prediction takes an instance (e.g., such as some patient symptoms in a medical diagnosis example) and generates a prediction set containing a set of labels expected to contain the true label with a user defined probability 1-alpha. Typically this coverage is expected to hold marginally over the randomness in the data.

To generate prediction sets, we take some held-out labeled data (which should be distinct from the model training or test sets), and for each instance in this calibration set, we take the value of a heuristic measure of prediction uncertainty that our model provides for the true label (this could be, e.g., a softmax score from the final layer of a neural net, or a residual in a regression setting). We convert this into a non-conformity score, i.e., a score that takes larger values the less “conforming” the label is from what the model has learned. For example, the score could be as simple as 1 – softmax(y) for label y. We then calculate the 1-alpha quantile of the non-conformity scores for the true labels in the calibration set. Given some new instance, we use this 1-alpha quantile as a threshold, including in the prediction set all the labels with non-conformity scores less than the threshold. 

Yifan Wu, Dawei Xie, Ziyang Guo, Andrew and I write:

Methods to quantify uncertainty in predictions from arbitrary models are in demand in high-stakes domains like medicine and finance. Conformal prediction has emerged as a popular method for producing a set of predictions with specified coverage on average, in place of a single top prediction and confidence value. However, the value of conformal prediction sets to assist human decisions remains elusive due to the murky relationship between coverage guarantees and decision makers’ goals and strategies. How should we think about conformal prediction sets as a form of decision support? We outline a decision theoretic framework for evaluating predictive uncertainty as informative signals, then contrast what can be said within this framework about idealized use of calibrated probabilities versus conformal prediction sets. Informed by prior empirical results and theories of human decision making under uncertainty, we formalize a set of possible strategies by which a decision maker might use a prediction set. We identify ways in which conformal prediction sets and post hoc predictive uncertainty quantification more broadly are in tension with common goals and needs in human-AI decision making. We give recommendations for future research in predictive uncertainty quantification to support human decision makers. 

What might decision makers do with prediction sets? 

In the paper, we contrast prediction uncertainty that has a well-defined use by a loss-minimizing rational decision maker (such as a calibrated probability, which the rational decision maker uses to update their beliefs then choose the action expected to minimize their loss), with conformal prediction, where the decision strategy that a risk-neutral rational decision maker should use is underspecified. Our goal is to characterize various strategies that decision makers might apply. Several of these have anecdotally come up in the literature or been mentioned by participants in studies we’ve run, but not formalized. 

For example, decision makers have reported using a prediction set to verify their own judgments. If we assume the decision maker has a prior probability distribution over labels (p(Y)), then upon seeing a prediction C_hat(x), for each possibly label y, the decision maker can update their beliefs by noting whether the label is in the set, normalizing its prior probability, then multiplying it by either 1-alpha (if in set) or alpha (if not). I.e., the posterior probability for all labels in the set C_hat(x) becomes (1-alpha) * p(y)/(sum of p(y’) for all y’ in C_hat(x)). For labels not in the set, we replace (1-alpha) with alpha and normalize each label’s prior probability by the sum of probabilities of all labels not in the set.

However, some decision makers might instead use sets to constrain their decisions, such as when a doctor rules in or out certain conditions based on what labels appear in a set. The simplest strategy for this kind of decision maker would be to just divide probability equally among all labels in the set and assign zero probability to all labels not in the set. However, we can also imagine more sophisticated strategies, for example that capture the intuition that prediction sets reduce the “cognitive cost” of making a decision. Here, we can look to a rational inattention model for economics, where the decision maker’s objective is to find the action that minimizes loss that incorporates a penalty term representing the cost of information acquisition (which in this case is the attentional cost associated with considering a label).  

We can also imagine variations on verify and constrain strategies where decision makers perceive labels as having some similarity relation over them. This was reported by study participants in our empirical work and figured as well as in recent work on decision-focused prediction sets. Medical conditions can be related based on how similar treatments or risk levels are. Labels for objects that appear in images can be related using semantic ontologies like the Wordnet hierarchy. Perceived similarities between labels might factor into how the decision maker uses sets or assigns value to them. For example, given some similarity function over labels, the decision maker might “transfer” probability from labels that appear in the set to similar labels that don’t.  

Shortly before I planned to post this paper, Kiyani, Pappas, Roth, and Hassani posted an interesting related paper asking what kind of decision process makes prediction sets the right way to communicate uncertainty. They show that when you have a risk averse (as opposed to risk neutral) decision maker who seeks to maximize their minimum utility despite ambiguity about the data-generating distribution, then a max-min rule is an optimal strategy for using prediction sets with marginal coverage, where the decision maker chooses the action that maximizes their utility in the worst case over label outcomes. They also show, somewhat surprisingly, that prediction sets contain all of the information necessary for this kind of risk-averse decision making. 

Questioning the usual restrictions on the decision maker’s knowledge

Another thing we discuss is how common reasons for involving human decision makers in the first place complicate the goal of producing valid uncertainty estimates. Namely, we are often hesitant to replace human decision makers completely with statistical models because we think they have some valuable knowledge to contribute over the information available to the model. The problem is that when we allow for the decision maker to potentially have access to some private information not available to the model, then for all we know, the calibrated uncertainty quantification we are so carefully trying to achieve may be the wrong information to provide. See for example this demonstration by Corvelo Benz and Rodriguez of how a calibrated model probability may not help the decision maker with access to private information optimize their choice of action. This tension is rarely acknowledged in theoretical and algorithmic computer science research on uncertainty quantification, so we devote some of our paper to spelling out the problem . 

Ways to better align conformal prediction with what we know about human decisions

We make some recommendations for how to better align research on conformal prediction with what we know about human decision making under uncertainty. This includes advice for empirically studying how decision makers use prediction sets, such as by formulating benchmarks representing expected performance under the different strategies we characterize and comparing observed human decision performance to them to try to tease apart what people are doing. We need to be looking for ways to design uncertainty quantification despite the potential mismatch in information access between the expert and model (e.g., by multicalibrating prediction uncertainty over the model and human’s information as described here). There is also a lot we still don’t know when it comes to how people respond to different properties of prediction sets. We can do a better job of informing aspects of prediction set design with preferences we elicit or learn from expert decisions, such as for the diversity of items in a set (i.e., should seeing a set ever prompt the decision maker to think more divergently than they otherwise would?) or the shape of prediction sets in higher dimensions. More generally, it’s possible that how human decision makers are informed by prediction sets is less sensitive to coverage than the conformal literature implies, in which case we should consider instead maximizing coverage subject to other constraints. If you’ve ever studied how people use confidence intervals, you’ll know what kinds of insensitivity I’m talking about. 

Why it’s hard to “price in” conformal prediction

We conclude with some thoughts on why it’s hard to appraise the value of different approaches to quantifying uncertainty, including post hoc prediction calibration methods like conformal prediction. One issue is that often the factors that drive the popularity of certain methods for quantifying uncertainty lie outside the bounds of theory. The standard bootstrap, for example, is widely used in part because it’s a simple concept that promises uncertainty quantification without much thinking, not necessarily because theorists can prove ways to improve convergence as sample size grows. Then there is the challenge of assigning value to certain forms of uncertainty that some decision makers may desire (e.g., Bayesian probability) because they don’t fit into the framework we’re working in (e.g., loss minimization; see prior post on this here). There are some things theory is hard pressed to comment on in current forms, but this doesn’t mean we should pretend they don’t exist.