Everyone’s trading bias for variance at some point, it’s just done at different places in the analyses

Some things I respect

When it comes to meta-models of statistics, here are two philosophies that I respect:

1. (My) Bayesian approach, which I associate with E. T. Jaynes, in which you construct models with strong assumptions, ride your models hard, check their fit to data, and then scrap them and improve them as necessary.

2. At the other extreme, model-free statistical procedures that are designed to work well under very weak assumptions—for example, instead of assuming a distribution is Gaussian, you would just want the procedure to work well under some conditions on the smoothness of the second derivative of the log density function.

Both the above philosophies recognize that (almost) all important assumptions will be wrong, and they resolve this concern via aggressive model checking or via robustness. And of course there are intermediate positions, such as working with Bayesian models that have been shown to be robust, and then still checking them. Or, to flip it around, using robust methods and checking their implicit assumptions.

I don’t like these

The statistical philosophies I don’t like so much are those that make strong assumptions with no checking and no robustness. For example, the purely subjective Bayes approach in which it’s illegal to check the fit of a model because it’a supposed to represent your personal belief. I’ve always thought this was ridiculous, first because personal beliefs should be checked where possible, second because it’s hard for me to believe that all these analysts happen to be using logistic regression, normal distributions, and all the other standard tools, out of personal belief. Or the likelihood approach, advocated by those people who refuse to make any assumptions or restrictions on parameters but are willing to rely 100% on the normal distributions, logistic regressions, etc., that they pull out of the toolbox.

Unbiased estimation is a snare and a delusion

Unbiased estimation used to be a big deal in statistics and remains popular in econometrics and applied economics. The basic idea is that you don’t want to be biased; there might be more efficient estimators out there but it’s generally more kosher to play it safe and stay unbiased.

But in practice one can only use the unbiased estimates after pooling data (for example, from several years). In a familiar Heisenberg’s-uncertainty-principle sort of story, you can only get an unbiased estimate if the quantity being estimated is itself a blurry average. That’s why you’ll see economists (and sometimes political scientists, who really should know better!) doing time-series cross-sectional analysis pooling 50 years of data and controlling for spatial variation using “state fixed effects.” That’s not such a great model, but it’s unbiased—conditional on you being interested in estimating some time-averaged parameter. Or you could estimate separately using data from each decade but then the unbiased estimates would be too noisy.

To say it again: the way people get to unbiasedness is by pooling lots of data. Everyone’s trading bias for variance at some point, it’s just done at different places in the analyses.

t seems (to me) to be lamentably common for classically-trained researchers to first do a bunch of pooling without talking about it, then getting all rigorous about unbiasedness. I’d rather fit a multilevel model and accept that practical unbiased estimates don’t in general exist.

B-b-b-but . . .

What about the following argument in defense of unbiased estimation: Sure, any proofs of unbiasedness are based on assumptions that in practice will be untrue—but, it makes sense to see how a procedure works under ideal circumstances. If your estimate is biased even under ideal circumstances, you got problems. I respect this reasoning but the problem is that the unbiased estimate doesn’t always come for free. As noted above, typically the price people pay for unbiasedness is to do some averaging, which at the extreme case leads to the New York Times publishing unreasonable claims about the Tea Party movement (which started in 2009) based on data from the cumulative General Social Survey (which started in 1972). I’m not in any way saying that the New York Times writer was motivated by unbiasedness, I’m just illustrating the real-world problems that can arise from pooling data over time.

Here’s the cumulative GSS:

And here are the data just from 2009-2010 (which is what is directly relevant to the Tea Party movement):

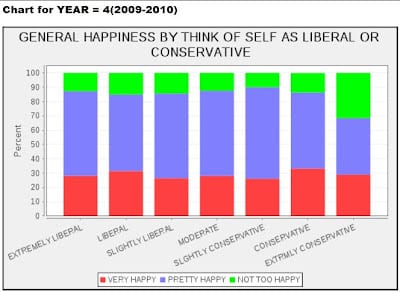
The choice to pool is no joke; it can have serious consequences. If we can avoid pooling, instead using multilevel modeling and other regularization techniques.

The tough-guy culture

There seems to be tough-guy attitude that is prevalent among academic economists, the idea that methods are better if they are more mathematically difficult. For many of these tough guys, Bayes is just a way of cheating. It’s too easy. Or, as they would say, it makes assumptions they’d rather not make (but I think that’s ok, see point 1 at the very top of this post). I’m not saying I’m right and the tough guys are wrong; as noted above, I respect approach 2 as well, even though it’s not what I usually do. But among many economists it’s more than that, I think it’s an attitude that only the most theoretical work is important, that everything else is stamp collecting. As I wrote a couple years ago, I think this attitude is a problem in that it encourages a focus on theory and testing rather than modeling and scientific understanding. It was a bit scary to me to see that when applied economists Bannerjee and Duflo wrote a general-interest overview paper about experimental economics, that when discussing data analysis, they cited papers such as this:

Bootstrap tests for distributional treatment effects in instrumental variables models Nonparametric tests for treatment effect heterogeneity Testing the correlated random coefficient model Asymptotics for statistical decision rules

I worry that the tough-guy attitude that Bannerjee and Duflo have inherited might not be allowing them to get the most out of their data–and that they’re looking in the wrong place when researching better methods. The problem, I think, is that they (like many economists) think of statistical methods not as a tool for learning but as a tool for rigor. So they gravitate toward math-heavy methods based on testing, asymptotics, and abstract theories, rather than toward complex modeling. The result is a disconnect between statistical methods and applied goals.

Lasso to the rescue?

One of the (many) things I like about Rob Tibshirani’s lasso method (L_1 regularization) is that it has been presented in a way that gives non-Bayesians (and, oddly enough, some Bayesians as well) permission to regularize, to abandon least squares and unbiasedness. I’m hoping that lasso and similar ideas will eventually make their way into econometrics—and that once they recognize that the tough guys in statistics have abandoned unbiasedness, the econometricians will follow, and maybe be more routinely open to ideas such as multilevel modeling that allow more flexible estimates of parameters that vary over time and across groups in the population.