“No Vehicles in the Park”: A multilevel-model computing saga (including some Bayesian workflow)
Statistical Modeling, Causal Inference, and Social Science 2025-04-14
This is a story about how hard it can be to fit even a simple multilevel model. It’s a long story, but that’s ok: we have a lot to think about:
1. The data and the problem 2. Fitting an item-response model using lme4 3. Understanding and expanding the fitted model 4. Fitting using rstanarm 5. The funnel rears its ugly head 6. Fitting the model using Stan 7. A model with 3 constant terms 8. Two simulation experiments 9. Summary of results 10. Other software options 11. Conclusion 12. How to write this up in a way to be most useful to readers?
It’s a story in twelve parts, but no Comedian, no Rorschach, not even a cartoon smiley face. It’s something I needed to work through, nevertheless.
1. The data and the problem
It began with this blog post by Dan Luu a couple of years ago, which pointed to an online quiz from Dave Turner that begins:
Every question is about a hypothetical park. The park has a rule: “No vehicles in the park.” Your job is to determine if this rule has been violated.
You might know of some rule in your jurisdiction which overrides local rules, and allows certain classes of vehicles. Please disregard these rules; the park isn’t necessarily in your jurisdiction. Or perhaps your religion allows certain rules to be overridden. Again, please answer the question of whether the rule is violated (not whether the violation should be allowed).
Then 27 questions follows with different scenarios; for example:
And you can see where you, and others, would draw the line. Turner generously shares this file with 51953 responses from 2409 people giving yes/no answers to the 27 questions. The columns are: • Submission id (a unique id for the respondent) • Question id (a unique id for each question) • Indicator if the person described in the survey question has a male-sounding name • Indicator if the person described in the survey question has a white-sounding name • Response (1 for the response, “Yes, this violates the rule” and 0 for the response, “No, this does not violate the rule”)
The wordings for the 27 items are here.
From some googling, I gather that the No Vehicles in the Park problem dates from a law review article by H. L. A. Hart from 1958 (see footnote 1 here), but I first heard about it from the above-linked post from Dan Luu.
Our goal here is to fit an item-response / ideal-point model including variation over respondents and items. In short: some respondents are more likely to answer Yes to these questions and some items are more likely to elicit Yes responses.
A lot can be done with these data, but our entire post here will be devoted to the statistically–but, as we shall see, not computationally–simple problem of estimating the very basic model of independent responses:
Pr(y_i=1) = invlogit(X_i*beta + a_{j[i]} – b_{k[i]}),
where i=1,…,51953 indexes the responses, j[i] indexes the person giving that response, k[i] indexes the item, and X is a 51953 x 4 matrix with 4 columns: • Constant term (that is, a column of 1’s) • Indicator for male-sounding name for item i • Indicator for white-sounding name for item i • The number of responses given by person j[i]. In this dataset about two-thirds of the respondents answered all 27 questions (they are rule-followers!), with most of the others answering between 7 and 26 items, and one person answering only 2 questions.
2. Fitting an item-response model using lme4
We start by setting up the data in R:
park <- read.csv("park.csv")N <- nrow(park)respondents <- sort(unique(park$submission_id))J <- length(respondents)respondent <- rep(NA, N)for (j in 1:J){ respondent[park$submission_id == respondents[j]] <- j}items <- sort(unique(park$question_id))K <- length(items)item <- park$question_idy <- park$answern_responses <- rep(NA, J)for (j in 1:J){ n_responses[j] <- sum(respondent==j)}male_name <- park$malewhite_name <- park$whiten_responses_full <- n_responses[respondent]And then we fit the model using lme4:
library("arm")data_matrix <- data.frame(y, respondent, item, male_name, white_name, n_responses_full)fit_lme4 <- glmer(y ~ (1 | item) + (1 | respondent) + male_name + white_name + n_responses_full, family=binomial(link="logit"), data=data_matrix)display(fit_lme4)Which yields:
coef.est coef.se(Intercept) -1.50 0.46 male_name 0.07 0.03 white_name 0.08 0.03 n_responses_full -0.03 0.01 Error terms: Groups Name Std.Dev. respondent (Intercept) 1.92 item (Intercept) 2.31 Residual 1.00 ---number of obs: 51953, groups: respondent, 2409; item, 27
The next step is to understand the estimated coefficients and error terms. Along the way to doing that, we'll run into some challenges.
3. Understanding and expanding the fitted model
3.1. Understanding the intercept
Going through the above output in order: - The intercept is -1.50. This corresponds to the prediction (on the logit scale) for a data point where all the predictors are zero . . . This is hard to interpret, given that n_responses_full is never zero: it usually takes on the value of 27. - Before going through the rest of the output, let's work to understand the intercept term. We could compute the predicted probability by setting n_responses_full=27, thus, invlogit(-1.50 - 0.03*27), but instead let's just code that last predictor in terms of the number of items skipped so that zero is a reasonable baseline:
n_skipped <- K - n_responses
We then re-fit the model:
n_skipped_full <- n_skipped[respondent]data_matrix <- data.frame(y, respondent, item, male_name, white_name, n_skipped_full)fit_lme4 <- glmer(y ~ (1 | item) + (1 | respondent) + male_name + white_name + n_skipped_full, family=binomial(link="logit"), data=data_matrix)display(fit_lme4)
Which yields:
coef.est coef.se(Intercept) -2.42 0.45 male_name 0.07 0.03 white_name 0.08 0.03 n_skipped_full 0.03 0.01 Error terms: Groups Name Std.Dev. respondent (Intercept) 1.92 item (Intercept) 2.31 Residual 1.00 ---number of obs: 51953, groups: respondent, 2409; item, 27
OK, so let's try again:
- For an average respondent given an average item, if that question is given with a female, nonwhite name and the respondent is someone who answered all 27 questions, the estimated probability of a "Yes, this violates the rule" response is invlogit(-2.42) = 0.08.
Just to check, I'll go the raw data:
> mean(y)[1] 0.238735
Huh? I'm surprised. This should be close to 0.08, no? OK, let me restrict just to the cases with zero values for the three predictors:
> mean(male_name==0 & white_name==0 & n_skipped_full==0)[1] 0.21
And it's not like this is an empty category:
> sum(male_name==0 & white_name==0 & n_skipped_full==0)[1] 10748
We can also compute the predicted probability for an average case:
> invlogit(-2.42 + 0.07*mean(male_name) + 0.08*mean(white_name) + 0.03*mean(n_skipped_full))[1] 0.09
This too is nothing close to the mean of the raw data.
At this point, I'm not quite sure what's going on here. It must have to do with the nonlinearity of the logit function: for an average case, the predicted probability is 0.09, but sometimes that probability is much higher or lower. At the low end it's bounded by zero, so the mean probability (rather than the probability of the mean) will be much more than 0.09.
Hey, we can check this by running the model in "predict" mode:
> mean(predict(fit_lme4, type="response"))[1] 0.23
So, yeah, it's the extreme nonlinearity of the logit when the predicted probability for an average case is near 0 (in this case, it's 0.09) and the variance on the logit scale is high (which it is; check out the high estimates for the standard deviations of the respondent and item effects above).
3.2. A simulated-data experiment
When in doubt, I like to check with fake data. Here it's easy enough to simulate from the fitted model. First we simulate the varying intercepts given the estimated variance parameters:
set.seed(123)a_respondent_sim <- rnorm(J, 0, sqrt(VarCorr(fit_lme4)$respondent))a_item_sim <- rnorm(K, 0, sqrt(VarCorr(fit_lme4)$item))
Then we throw in the estimated regression coefficients and pipe it through the logit:
b_sim <- fixef(fit_lme4)X <- cbind(1, male_name, white_name, n_skipped_full)p_sim <- invlogit(a_respondent_sim[respondent] + a_item_sim[item] + X %*% b_sim)y_sim <- rbinom(N, 1, p_sim)
Next we add the simulated responses to the data frame and re-fit the model:
data_sim <- data.frame(data, y_sim)fit_lme4_sim <- glmer(y_sim ~ (1 | item) + (1 | respondent) + male_name + white_name + n_responses_full, family=binomial(link="logit"), data=data_sim)display(fit_lme4_sim)
And here's what pops out:
coef.est coef.se(Intercept) -1.88 0.53 male_name 0.06 0.03 white_name 0.12 0.03 n_responses_full -0.04 0.01 Error terms: Groups Name Std.Dev. respondent (Intercept) 1.87 item (Intercept) 2.65 Residual 1.00 ---number of obs: 51953, groups: respondent, 2409; item, 27
The parameter estimates are within a standard error of what came before . . . I guess the real question is why is the standard error for the intercept so high?
The standard error for the intercept is 0.45 (or 0.41 when fit to the simulated data); this seems huge for a logistic regression fit to 52,000 data points.
The fitting challenge here has got to be coming from those 27 item parameters: a high variance and only K=27 will lead to some uncertainty in the rest of the fitted model.
Let's look at those 27 estimates:
> a_item_hat <- ranef(fit_lme4)$item> print(a_item_hat) (Intercept)1 7.6072 3.0093 -0.7384 -1.0165 1.1556 -0.9707 -0.5088 1.9869 3.23210 1.34411 -1.25412 -3.17113 0.48914 -1.23915 -0.58616 0.61017 -2.78318 -1.59319 0.02220 -2.79321 1.03822 0.29523 -0.04524 -1.49125 -0.03926 -0.50327 2.008> options(digits=1)> a_item_hat <- ranef(fit_lme4)$item> print(a_item_hat) (Intercept)1 7.612 3.013 -0.744 -1.025 1.156 -0.977 -0.518 1.999 3.2310 1.3411 -1.2512 -3.1713 0.4914 -1.2415 -0.5916 0.6117 -2.7818 -1.5919 0.0220 -2.7921 1.0422 0.3023 -0.0524 -1.4925 -0.0426 -0.5027 2.01
Ummm, hard to read these. Let's extract the item names and attach them to those numbers:
wordings <- read.csv("park.txt", header=FALSE)$V2wordings <- s ubstr(wordings, 2, nchar(wordings)-1)a_item_hat <- unlist(a_item_hat)names(a_item_hat) <- wordingsThe space in "s ubstr" above is there to defeat Columbia's stupid firewall which is otherwise blocking this post. There should be no such space in the code.
Anyway, we can now print the estimates in order:
> sort(a_item_hat) kite paper_airplane iss toycar ice_skates -3.17 -2.79 -2.78 -1.59 -1.49 toyboat parachute plane surfboard skates -1.25 -1.24 -1.02 -0.97 -0.74 skateboard_carried wheelchair stroller travois sled -0.59 -0.51 -0.50 -0.05 -0.04 rccar horse quadcopter skateboard wagon_kids 0.02 0.30 0.49 0.61 1.04 wagon rowboat bike memorial ambulance 1.15 1.34 1.99 2.01 3.01 police car 3.23 7.61
Interesting. The distribution for these items is far from normal. Almost everybody thinks the private car violates the rule, and most people think the same about the police car and the ambulance (???), while, at the other extreme, just about everybody's cool with the kite, the paper airplane, and the space station flying above. I'm actually kinda surprised that these coefficients aren't even further away from zero . . . let's compare these estimated item effects to the raw averages:
item_avg <- rep(NA, K)for (k in 1:K) { item_avg[k] <- mean(y[item==k])}plot(item_avg, a_item_hat, pch=20)Here's the resulting graph:
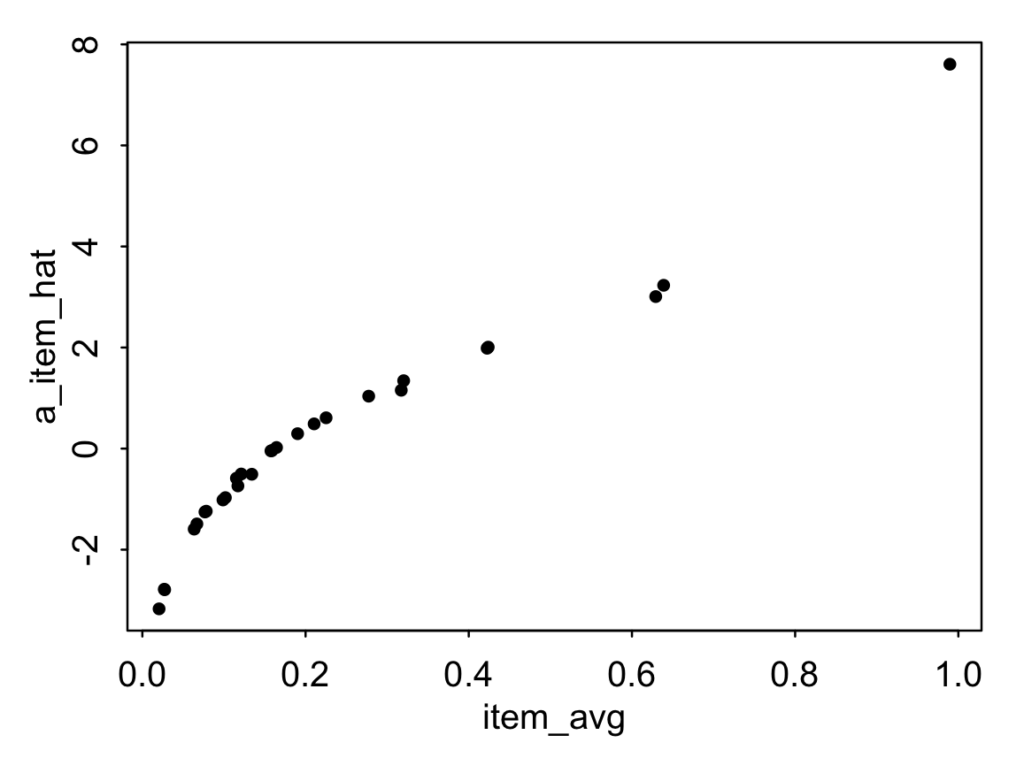
The raw rates range from 2% saying that the kite violates the rule to 99% saying that car violates the rule. Again, it's surprising to me these aren't 0% and 100% but maybe some respondents were taking the piss.
I'll re-plot labeling the points and on the logit scale:
plot(logit(item_avg), a_item_hat, type="n")text(logit(item_avg), a_item_hat, names(a_item_hat), cex=.5)

You can't read all the items but you get the basic idea.
For the purpose of estimating these parameters we didn't really need the item-response model, but that's because the data are balanced: people were given the items randomly. In general with this sort of rating problem, it's important to fit this sort of model to account for systematic differences in who rates which items.
Just for laffs we can look at the parameter estimates and data averaged by respondents:
a_respondent_hat <- unlist(ranef(fit_lme4)$respondent)respondent_avg <- rep(NA, J)for (j in 1:J) { respondent_avg[j] <- mean(y[respondent==j])}plot(respondent_avg, a_respondent_hat, pch=20, cex=.4)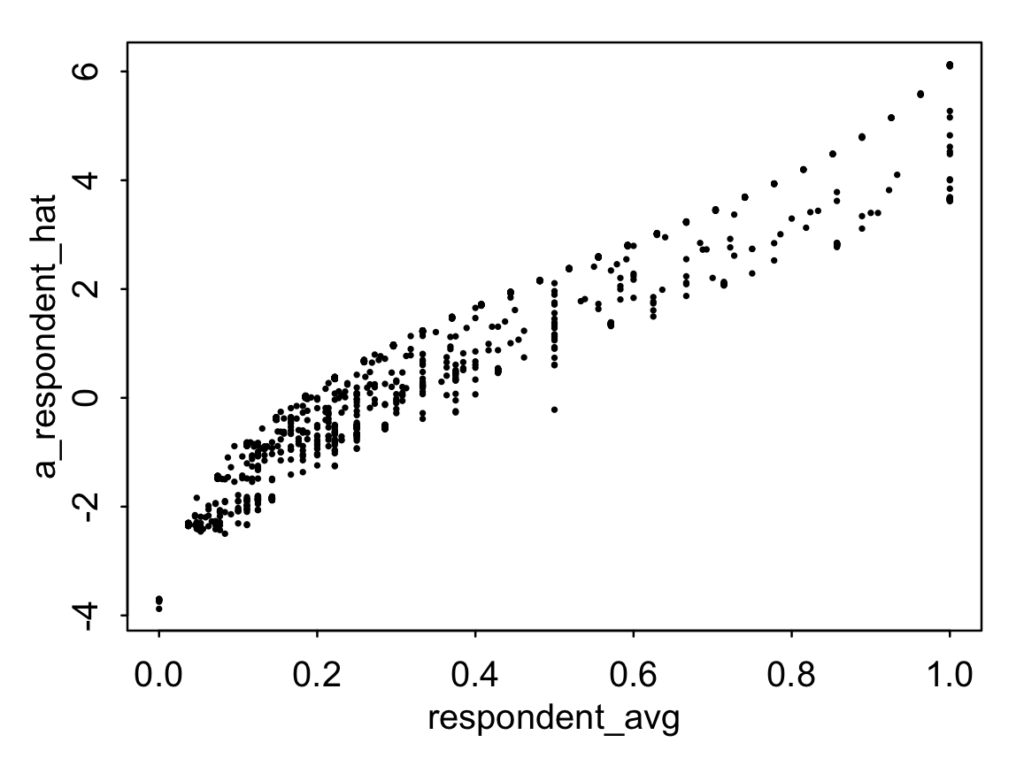
We can see a few things from the graph: - Some number of respondents answered Yes or No to all the items. From this graph we can't see how many because of overplotting, but we can just compute sum(respondent_avg==1) and sum(respondent_avg==0) directly and find that 38 people answered Yes to all their items (that is, saying the No Vehicles in the Park rule always applies) and 10 answered only No (that is, saying that the rule never applies). - There's quite a bit of variation in how people respond--this is something we can also see from the large value for the estimated variation of these intercepts in the fitted model. - There's some variation in the scatterplot, which is mostly coming from variation in the number of items that people answered. The fewer items you answer, the more your intercept is partially pooled toward the mean of the distribution (zero, in this case).
3.3. Understanding the fitted model
OK, that was a real rabbit hole! Now let's return to the fitted multilevel logistic regression, fit_lme4
coef.est coef.se(Intercept) -2.42 0.45 male_name 0.07 0.03 white_name 0.08 0.03 n_skipped_full 0.03 0.01 Error terms: Groups Name Std.Dev. respondent (Intercept) 1.92 item (Intercept) 2.31 Residual 1.00 ---number of obs: 51953, groups: respondent, 2409; item, 27
Going through the table from the top: - We've already talked about the intercept. - The coefficient for male_name is 0.07: people in this experiment are slightly more likely to say that someone with a male name is violating the rules. This is a small effect (and, yes, we can legitimately call it an "effect," as I'm pretty sure that the "treatment" of using a male or female name was assigned at random), shifting the estimated probability of "Yes, this violates the rule" from 0.24 (recall, that's the mean of y in the data) to invlogit(logit(0.24) + 0.07) = 0.253. - The coefficient for white_name is 0.08: people in this experiment are slightly more likely to say that someone with a white name is violating the rules: again, the estimated effect is small, an estimated increased of 1.5 percentage points in the probability of a Yes response. - People who skipped more questions are more likely to say, "Yes, this violates the rule." This effect is not so small: comparing a person who skipped 10 questions to someone who skipped none, the predicted probability of saying Yes increases from 0.24 to invlogit(logit(0.24) + 0.03*10) = 0.30.
This is kind of interesting, and it makes me think that we should also include in the model a predictor for the order in which the questions were asked. Perhaps there's a trend where, as the questions go on, people are increasingly likely to answer No.
So I'll create that new predictor:
order_of_response <- rep(NA, N)for (j in 1:J) { order_of_response[respondent==j] <- 1:n_responses[j]}data_matrix <- data.frame(data_matrix, order_of_response)And add it to the model:
fit_lme4 <- glmer(y ~ (1 | item) + (1 | respondent) + male_name + white_name + n_skipped_full + order_of_response, data=data, family=binomial(link="logit"))display(fit_lme4)
Here's the result:
coef.est coef.se(Intercept) -2.59 0.45 male_name 0.07 0.03 white_name 0.08 0.03 n_skipped_full 0.04 0.01 order_of_response 0.01 0.00 Error terms: Groups Name Std.Dev. respondent (Intercept) 1.92 item (Intercept) 2.33 Residual 1.00 ---number of obs: 51953, groups: respondent, 2409; item, 27
So, no, order of response (a predictor that varies from 1 to 27 in the data) doesn't seem to do much here. Good to know.
We conclude our understanding of the fitted model by interpreting the error variances. The distributions of respondent and item intercepts have estimated standard deviations of around 2, which is a big number on the logit scale: roughly speaking, the model estimates that about two-thirds of respondent intercepts are in the range (-1.92, 1.92), and about two-thirds of item intercepts are in the range (-2.33, 2.33). A shift of +/- 2 on the logit scale is big when you convert it to probabilities. If we start with that probability of 0.24, subtracting or adding 2 on the logit scale takes you to invlogit(logit(0.24) - 2) = 0.05 or invlogit(logit(0.24) + 2) = 0.70 on the probability scale. So, as we've already seen in the above graph, there's lots of variation across respondents and items.
4. Fitting using stan_glmer
All the above is fine. Sometimes, though, lme4 doesn't work so well. It can yield degenerate estimates for varying-intercept, varying slope models (see for example here) and, more generally, has the usual problems of point estimation that it understates uncertainty and can produce noisy estimates. So by default we prefer to use Stan, even if it's a little bit slower.
That's easy to do here using rstanarm, so first we load in that package and set it up to run parallel chains:
library("rstanarm")options(mc.cores = parallel::detectCores())And then we fit the model:
fit_rstanarm <- stan_glmer(y ~ (1 | item) + (1 | respondent) + male_name + white_name + n_skipped_full + order_of_response, family=binomial(link="logit"), data=data_matrix)print(fit_rstanarm)
But in this case it takes forever. It takes so long that I hit the escape key, restarted R, and ran a minimal version:
fit_rstanarm <- stan_glmer(y ~ (1 | item) + (1 | respondent) + male_name + white_name + n_skipped_full + order_of_response, family=binomial(link="logit"), data=data_matrix, iter=200, control=list(max_treedepth=5))print(fit_rstanarm)
There's an annoyance in the stan_glmer syntax where the number of iterations is set in one part of the function call and the treedepth is set elsewhere. This is a legacy of the rstanarm package using rstan rather than the newer interface, cmdstanr. The control options are cleaner when running Stan programs directly using cmdstanr, as we'll see below.
Anyway, to return to our main narrative, when we ran stan_glmer for 100 iterations and max treedepth of 5 and (by default) 4 chains, it's fast, but the chains do not mix well, and we get a long warning message, including this:
The largest R-hat is 4.34, indicating chains have not mixed.Markov chains did not converge! Do not analyze results!
Rather than chugging through thousands of iterations, I paused to think for a moment, and, from my experience fitting multilevel models, I realized the problem. It's subtle, involving both modeling and computing.
5. The funnel rears its ugly head
The problem is "the funnel," also called "the whirlpool," "the vortex," and a few other things, and it comes up with group-level variance parameters in multilevel models. David van Dyk, Zaiying Huang, John Boscardin, and I discuss the problem in this paper from 2008: the usual parameterization of the Gibbs sampler or Metropolis algorithm for such problems can get stuck when the estimated group-level variance is near zero, and the alternative, "non-centered" parameterization, can get stuck when the estimated group-level variance is near infinity. This discussion from an old version of the Stan User's Guide demonstrates the problem in a simple special case. In our 2008 paper, we recommended a redundant parameterization that works in an expanded parameter space, but this doesn't work so well with Stan, because it involves a renormalization of the parameters at each iteration.
We do not (yet) have a universal solution to the funnel problem. Here are a few options, along with their strengths and weaknesses. I'll discuss them in the context of a simple varying-intercept model with measurements i and groups j[i]:
y_i ~ normal(a_{j[i]} + X_i*beta, sigma_y), i=1,...,n a_j ~ normal(mu, sigma_a), j=1,...,J
1. Standard parameterization as above. Works fine if sigma_a is well estimated from data and distinct from zero but runs into problems when there is posterior mass near zero, as in the 8 schools example from chapter 5 of BDA. The problem here is that in multilevel modeling you typically want sigma_a to become indistinguishable from zero: that's desirable behavior if you include high-quality group-level predictors in X.
2. Alternative parameterization:
y_i ~ normal(mu + sigma_a*xi_{j[i]} + X_i*beta, sigma_y), i=1,...,n xi_j ~ normal(0, 1), j=1,...,J
This is mathematically the same model as above, but now it's parameterized in terms of sigma_a and xi rather than sigma_a and a = mu + sigma_a*xi. This fixes the geometry of the posterior distribution near sigma_a=0, allowing HMC (or Gibbs or Metropolis) to slide up and down the "cone" of the joint distribution rather than getting struck in the "vortex." The alternative parameterization works just fine with the 8 schools, as demonstrated in Appendix C of BDA, and other problems where there is only weak information on the group-level scale parameter sigma_a. The bad news is that it fails in the opposite scenario in which sigma_a is well estimated with a posterior distribution that is distinct from zero.
3. Redundant parameterization:
y_i ~ normal(mu + kappa*xi_{j[i]} + X_i*beta, sigma_y), i=1,...,n xi_j ~ normal(0, tau), j=1,...,J
This model on (kappa, tau, xi) does not separately identify kappa or tau, but it does identify their product. As we discuss in our 2008 paper, you can do Gibbs or Metropolis on this larger space and just re-compute sigma_a = kappa*tau and a = mu + kappa*xi at each iteration, and it works for both the problematic examples discussed above, along with everything in between! The bad news is that if you try this redundant parameterization in Stan or other Hamiltonian Monte Carlo (HMC)-based probabilistic programming languages, it will fail because there's no joint distribution in the probability space: HMC will just drift and never converge. And you can't even run non-convergent HMC on (kappa, tau, xi) and hope to get good inferences for the generated quantities (sigma_a, a),
4. Alternate between standard and alternative parameterizations:
The redundant parameterization includes the standard and alternative parameterizations as special cases (kappa=1 and tau=1, respectively). So, instead of jointly estimating (kappa, tau, xi), you can slide back and forth between the two parameterizations, which should give you something like 50% efficiency: not as good as the optimal parameterization for your problem but not getting stuck in the bad parameterization. This approach has two challenges: first, it makes the algorithm more complicated, especially given the problems of tuning the step size and mass matrix for HMC; second, in more complicated multilevel models with more than one grouping factor (as in the example that motivated this post!), you need to do this for each batch of parameters.
5. Decide which of the standard or alternative parameterizations to use based on a preliminary analysis of the data. As we shall see, this can work in practice--you can pick one parameterization, try it, and if you have convergence problems you can switch to the other--but it's awkward. And, again, this can run into combinatorial difficulties if you have multiple grouping factors.
6. Use a zero-avoiding and infinity-avoiding prior to rule out the bad areas of the funnel. This can work, but it's not always easy: There's no generic prior that will always solve the problem, and you have to be careful not to rule out zones in parameter space that you actually want to keep in the posterior.
7. Fit using the marginal posterior mode of the group-level variance parameter. The joint mode won't work (it has a pole at (sigma_a=0, a=mu); this is a well-known problem discussed in chapter 5 of BDA and elsewhere), but you can work with the marginal mode of sigma_a. That's what lme4 does. This works fine in the example that motivated this post, but, for harder problems, marginal-mode inference can be unstable. It often yields degenerate estimates, especially when the model includes varying slopes as well as intercepts, and even when the estimated variance parameters are not on the boundary, they can be noisy. These problems can be addressed with zero-avoiding priors (see our papers from 2013 and 2014), but then that's another required step. Indeed, one reason we wrote Stan in the first place was that lme4 was giving us problems when our models started to get complicated.
8. Other approximate algorithms. ADVI and Pathfinder are already programmed in Stan, and soon we'll have nested Laplace, which is pretty similar to lme4. These options could work well; I'll have to try them out. For now I'll just have to say they're untested, and, given that they are not trying to fully explore the posterior distribution, I expect they'll have problems.
9. New HMC implementations. Bob Carpenter has been talking about a new sampler that auto-adapts in a way so that it fits the funnel just fine. Maybe this will be in Stan soon and solve all our funnel problems?
10. Some combination of the above solutions. For example: start with a stable fast algorithm such as Pathfinder, include zero-avoiding and infinity-avoiding priors as necessary, run the new adaptive HMC algorithm, also be willing to change the parameterization if it's still running slowly. This would not represent a perfectly automatic solution but could still be a reliable workflow.
11. Resolve computing problems by simplifying the model. A big challenge with the funnel is when the unexplained group-level variance is statistically indistinguishable from zero. That's what happens in the 8 schools example. One solution here is to just set the group-level scale to zero--that is, to remove that batch of parameters from the model entirely. That's equivalent to partially pooling the group estimates all the way to the fitted model: in this setting, the model is difficult to fit in part because there's no much there to be estimated, so why not simplify? In other cases, you might be uncomfortable partially pooling all the way down, so you could pin the group-level scale to some small value--for example, sigma_a=5 in the 8 schools model--which will get rid of the funnel problem. The drawback to this approach is that it requires further human intervention and also is changing the model you're fitting.
6. Fitting the model using Stan
To return to our main thread . . . we're trying to fit the model with respondent and item effects. We had problems with rstanarm so let's try using straight-up Stan which will give us more flexibility in coding.
We put our first try into a file, park_1.stan:
data { int N, J, K, L; array[N] int y; array[N] int respondent; array[N] int item; matrix[N,L] X;}parameters { vector[L] b; real sigma_respondent, sigma_item; vector[J] a_respondent; vector[K] a_item;}model { a_respondent ~ normal(0, sigma_respondent); a_item ~ normal(0, sigma_item); y ~ bernoulli_logit(X*b + a_respondent[respondent] + a_item[item]);}This uses the alternative parameterization, scaling the respondent and item effects in proportion to their scale parameters, so I'm pretty sure that it will fail, just as the version from rstanarm failed. But we'll check.
In R, we set up the design matrix and the data list to be sent to Stan:
X <- cbind(rep(1,N), male_name, white_name, n_skipped_full, order_of_response)stan_data <- list(N=N, J=J, K=K, L=ncol(X), y=y, respondent=respondent, item=item, X=X)
Then we compile and run; to be on the safe side we just do 100 warmup and 100 saved iterations per chain and set max_treedepth=5:
library("cmdstanr")park_1 <- cmdstan_model("park_1.stan")fit_1 <- park_1$sample(data=stan_data, parallel_chains=4, iter_warmup=100, iter_sampling=100, max_treedepth=5)print(fit_1)Here's the (bad) result:
variable mean median sd mad q5 q95 rhat ess_bulk ess_tail lp__ -23496.85 -22783.60 1468.31 332.40 -26998.40 -22548.48 2.95 4 12 b[1] -1.14 -1.14 0.18 0.23 -1.37 -0.79 2.41 5 21 b[2] 0.03 0.03 0.02 0.02 0.00 0.07 1.02 69 175 b[3] 0.03 0.03 0.03 0.03 -0.01 0.08 1.09 61 117 b[4] 0.03 0.02 0.00 0.00 0.02 0.03 1.19 15 48 b[5] -0.01 -0.01 0.02 0.02 -0.04 0.01 2.88 4 12 sigma_respondent 0.06 0.06 0.01 0.01 0.05 0.07 2.18 5 12 sigma_item 1.08 1.16 0.28 0.28 0.55 1.39 3.07 4 14 a_respondent[1] -0.01 -0.01 0.05 0.04 -0.10 0.06 3.06 4 12 a_respondent[2] -0.03 -0.03 0.06 0.09 -0.12 0.05 3.94 4 12. . .
It still has problems if you run longer. For example this is what you get if you do the default 1000 warmup plus 1000 saved iterations per chain, again setting max_treedepth=5:
variable mean median sd mad q5 q95 rhat ess_bulk ess_tail lp__ -15146.77 -15098.70 133.90 77.98 -15415.81 -15004.80 1.60 6 11 b[1] -2.66 -2.71 0.34 0.24 -3.12 -1.96 1.55 8 43 b[2] 0.08 0.08 0.03 0.03 0.02 0.12 1.09 31 463 b[3] 0.07 0.07 0.03 0.04 0.02 0.13 1.24 12 76 b[4] 0.04 0.04 0.01 0.00 0.03 0.04 1.08 186 616 b[5] 0.01 0.01 0.00 0.00 0.01 0.02 1.04 444 1399 sigma_respondent 1.92 1.94 0.07 0.06 1.80 2.01 1.54 7 12 sigma_item 2.40 2.35 0.31 0.28 1.99 3.00 1.22 14 64 a_respondent[1] 0.21 0.32 1.80 1.79 -2.93 3.08 1.23 12 25 a_respondent[2] -0.41 -0.43 0.67 0.69 -1.48 0.63 1.03 144 1040. . .
The estimated group-level variances are big here, so it makes sense to use the standard parameterization, which is actually simpler to code in Stan. Here it is, in the file park_2.stan:
data { int N, J, K, L; array[N] int y; array[N] int respondent; array[N] int item; matrix[N,L] X;}parameters { vector[L] b; real sigma_respondent, sigma_item; vector[J] a_respondent; vector[K] a_item;}model { a_respondent ~ normal(0, sigma_respondent); a_item ~ normal(0, sigma_item); y ~ bernoulli_logit(X*b + a_respondent[respondent] + a_item[item]);}We'll fit this to our data, running 1000 warmup plus 1000 saved iterations per chain, max_treedepth=5:
park_2 <- cmdstan_model("park_2.stan")fit_2 <- park_2$sample(data=stan_data, parallel_chains=4, max_treedepth=5)print(fit_2)It takes 100 seconds to run on my laptop, and here's what comes out:
variable mean median sd mad q5 q95 rhat ess_bulk ess_tail lp__ -16718.24 -16717.70 39.66 39.88 -16783.80 -16652.80 1.02 324 921 b[1] -2.64 -2.58 0.50 0.52 -3.49 -1.82 1.43 8 13 b[2] 0.07 0.07 0.03 0.03 0.02 0.12 1.01 425 1137 b[3] 0.08 0.08 0.03 0.03 0.03 0.13 1.01 557 1135 b[4] 0.04 0.04 0.01 0.01 0.03 0.04 1.01 175 413 b[5] 0.01 0.01 0.00 0.00 0.01 0.02 1.00 863 1314 sigma_respondent 1.96 1.96 0.04 0.04 1.89 2.03 1.04 145 280 sigma_item 2.53 2.49 0.38 0.37 2.00 3.21 1.01 648 896 a_respondent[1] -0.39 -0.35 1.76 1.74 -3.41 2.49 1.01 417 956 a_respondent[2] -0.36 -0.32 0.70 0.66 -1.58 0.71 1.01 509 548. . .
Not so nice! We can run it in full default setting (4 chains, 1000 warmup plus 1000 saved iterations per chain, max_treedepth=10):
fit_2 <- park_2$sample(data=stan_data, parallel_chains=4)print(fit_2)
It now isn't too bad:
variable mean median sd mad q5 q95 rhat ess_bulk ess_tail lp__ -16714.93 -16715.20 39.87 39.88 -16780.50 -16650.59 1.00 1213 1805 b[1] -2.53 -2.53 0.51 0.48 -3.40 -1.72 1.02 195 233 b[2] 0.07 0.07 0.03 0.03 0.02 0.12 1.00 6622 3208 b[3] 0.08 0.08 0.03 0.03 0.03 0.14 1.00 7494 2747. . .
But it took 8 minutes to run. 8 minutes!
If you know what model you want to fit, and you're not worried about any problems in the data or whatever, then, sure, 8 minutes is fine, it's basically nothing. It took me a lot more than 8 minutes just to write material in this section of this post.
But if you're not sure exactly what you're planning to do, if you want to explore different models, if you want to do the usual Bayesian workflow, then you don't want to wait minutes. Not if you can avoid it.
7. A model with 3 constant terms
So what's going wrong here? We used the standard parameterization for the multilevel model, which should work better when the estimated group-level variance is large--and indeed we're now seeing better mixing for sigma_respondent and sigma_item, the group-level variance parameters--but now there's a problem with b[1], the coefficient for the constant term in the regression.
The intercept b[1] is identified in the model. The respondent effects and item effects both have distributions with mean 0. To put it another way, suppose the model were set up with:
a_respondent ~ normal(mu_respondent, sigma_respondent); a_item ~ normal(mu_item, sigma_item);
Then the posterior distribution would be improper: the parameters b[1], mu_respondent, and mu_item would not be identified. To put it another way, the model would have a translation invariance, as you could add any arbitrary constants to mu_respondent and mu_item and subtract these constants from b[1] without changing the target function. By setting mu_respondent and mu_item to zero:
a_respondent ~ normal(0, sigma_respondent); a_item ~ normal(0, sigma_item);
we've removed this invariance: the respondent and item effects are softly constrained toward zero. The constraint is "soft" rather than "hard" on the a_respondent and a_item parameters because the hard constraint is on the mean of their distribution; conditional on sigma_respondent and sigma_item, the respondent and item effects have informative priors centered at zero.
But . . . the soft constraint is not enough in this problem. Or, to put it more precisely, it's enough to identify the parameters but not enough to ensure smooth computation. In this model there are high posterior correlations between b[1], sum(a_respondent), and sum(a_item), and it's hard for our Hamiltonian Monte Carlo in its default settings to move efficiently in this space. Stan does some adaptation, but I think the adaptation is on the diagonal of the mass matrix so it doesn't correct for the correlations.
What to do?
I mentioned this problem to some colleagues, and they suggested using Stan's new sum_to_zero_vector type, as explained in this case study from Mitzi Morris. Here's how it works in the No Vehicles in the Park example--I put it in the file park_3.stan:
data { int N, J, K, L; array[N] int y; array[N] int respondent; array[N] int item; matrix[N,L] X;}parameters { vector[L] b; real sigma_respondent, sigma_item; sum_to_zero_vector[J] a_respondent; sum_to_zero_vector[K] a_item;}model { a_respondent ~ normal(0, sigma_respondent); a_item ~ normal(0, sigma_item); y ~ bernoulli_logit(X*b + a_respondent[respondent] + a_item[item]);}Here's the R code:
park_3 <- cmdstan_model("park_3.stan")fit_3 <- park_3$sample(data=stan_data, parallel_chains=4, max_treedepth=5)print(fit_3)It runs in 100 seconds with this perfect mixing:
variable mean median sd mad q5 q95 rhat ess_bulk ess_tail lp__ -16714.82 -16714.70 38.92 38.99 -16779.30 -16651.30 1.00 1137 1894 b[1] -2.60 -2.60 0.06 0.06 -2.70 -2.50 1.00 2237 2939 b[2] 0.07 0.07 0.03 0.03 0.02 0.12 1.00 7398 3227 b[3] 0.08 0.08 0.03 0.03 0.03 0.13 1.00 9024 2887 b[4] 0.04 0.04 0.01 0.01 0.03 0.05 1.00 1426 2576 b[5] 0.01 0.01 0.00 0.00 0.01 0.02 1.00 4123 3391 sigma_respondent 1.95 1.95 0.04 0.04 1.89 2.02 1.00 2023 2919 sigma_item 2.48 2.44 0.38 0.36 1.96 3.14 1.00 8438 2806 a_respondent[1] -0.33 -0.28 1.72 1.75 -3.20 2.47 1.00 2998 2964 a_respondent[2] -0.36 -0.34 0.67 0.67 -1.51 0.71 1.00 5091 2466. . .
That's a win!
There is some awkwardness to this model: with the sum of the respondent and item effects constrained to zero, some extra mathematical effort is required when making inferences for new items and new respondents.
8. Two simulation experiments
I'm curious about a couple of things here. First, is this weak-identification thing a problem with this particular dataset or would it arise with data simulated from the model? Second, yeah yeah I get it that the correlations cause a problem with the non-sum-to-zero model, but does this also have something to do with the nonlinearity of the logit?
We can answer--or, at least, study--both these questions using simulation, first by simulating data from the fitted multilevel logistic model, second by fitting the normal rather than logit model.
First the simulation. We'll use the simulated data y_sim from Section 3.2 above and then try fitting all these models:
stan_data_sim <- stan_datastan_data_sim$y <- y_simfit_1_sim <- park_1$sample(data=stan_data_sim, parallel_chains=4, max_treedepth=5)print(fit_1_sim)fit_2_sim <- park_2$sample(data=stan_data_sim, parallel_chains=4, max_treedepth=5)print(fit_2_sim)fit_3_sim <- park_3$sample(data=stan_data_sim, parallel_chains=4, max_treedepth=5)print(fit_3_sim)
Yeah, I know my code is ugly. Feel free to clean it for your own use.
Anyway, here's what happens: - As before, all three models took 100 seconds on my laptop. - park_1, the model with the alternative parameterization for the group-level variance, again shows poor mixing. Not as bad as with the real data, but still unacceptable for most practical purposes. - park_2, the model with the natural parameterization, does better but still shows poor mixing for the intercept, b[1], with an R-hat of 1.3. - park_3, the model with the sum_to_zero constraint, has essentially perfect convergence.
So the problem was with the model, not just with the data.
Next the normal model. We could simulate data from the normal distribution, but let's just try fitting the same item-response model as before, just with a normal error term. This seems weird given that the data are binary, but we can do it. Here's the new model, park_1_normal.stan:
data { int N, J, K, L; vector[N] y; array[N] int respondent; array[N] int item; matrix[N,L] X;}parameters { vector[L] b; real sigma_respondent, sigma_item, sigma_y; vector[J] a_respondent; vector[K] a_item;}model { a_respondent ~ normal(0, sigma_respondent); a_item ~ normal(0, sigma_item); y ~ normal(X*b + a_respondent[respondent] + a_item[item], sigma_y);}This is the same as before, except: (a) we changed the specification of y from integer array to vector, (b) we added sigma_y as a parameter, and (c) we changed the data model from bernoulli_logit to normal.
We create park_2_normal.stan and park_3_normal.stan in the same way, then we compile and run all three:
park_normal <- list(cmdstan_model("park_1_normal.stan"), cmdstan_model("park_2_normal.stan"), cmdstan_model("park_3_normal.stan"))fit_normal <- as.list(rep(NA, 3))for (i in 1:3){ fit_normal[[i]] <- (park_normal[[i]])$sample(data=stan_data, parallel_chains=4, max_treedepth=5) print(fit_normal[[i]])}Each one of these takes 70 seconds on my laptop--computing the gradient for the normal is a bit faster than for the logistic function, but for whatever reason it doesn't save much in compute time.
How did the computation go? Almost the same as before. Model 1 had terrible mixing, model 2 had poor mixing, but model 3 had some issues too:
variable mean median sd mad q5 q95 rhat ess_bulk ess_tail lp__ 38745.21 38745.60 35.71 36.03 38685.09 38801.40 1.01 408 760 b[1] 0.20 0.20 0.00 0.00 0.19 0.21 1.03 114 392 b[2] 0.00 0.00 0.00 0.00 0.00 0.01 1.00 386 1073 b[3] 0.01 0.01 0.00 0.00 0.00 0.01 1.01 570 973 b[4] 0.00 0.00 0.00 0.00 0.00 0.00 1.09 37 68 b[5] 0.00 0.00 0.00 0.00 0.00 0.00 1.02 216 643 sigma_respondent 0.19 0.19 0.00 0.00 0.18 0.19 1.01 867 1550 sigma_item 0.23 0.23 0.03 0.03 0.18 0.29 1.04 135 207 sigma_y 0.30 0.30 0.00 0.00 0.30 0.31 1.00 3670 2827 a_respondent[1] -0.04 -0.04 0.13 0.13 -0.25 0.17 1.02 124 294. . .
This time I think the problem was with the data.
We can check with a simple simulation experiment. First we simulate data from the above-fitted model, using the posterior medians of the parameters b, sigma_respondent, sigma_item, and sigma_y, then simulating the vectors a_respondent and a_item, then simulating new data from the normal model:
library("posterior")sims <- as_draws_rvars(fit_normal[[3]]$draws())a_respondent_sim <- rnorm(J, 0, median(sims$sigma_respondent))a_item_sim <- rnorm(K, 0, median(sims$sigma_item))b_sim <- median(sims$b)sigma_y_sim <- median(sims$sigma_y)y_sim <- rnorm(N, a_respondent_sim[respondent] + a_item_sim[item] + X %*% b_sim, sigma_y_sim)We then fit the three Stan models to this simulated dataset:
stan_data_sim$y <- y_simfit_normal_sim <- as.list(rep(NA, 3))for (i in 1:3){ fit_normal_sim[[i]] <- (park_normal[[i]])$sample(data=stan_data_sim, parallel_chains=4, max_treedepth=5) print(fit_normalsim[[i]])}Again, each model runs in about 70 seconds. Model 1 mixes terribly, model 2 again has problems with b[1], model 3 mixes ok, not great. Actually there's poor mixing for b[4], which is the coefficient for n_skipped. I'm really not sure why, also not sure why there's a problem for the normal model and not the binomial. That's why we do experiments--because things don't always go as expected! If you run it at default settings, mixing is fine but then it does take several minutes.
9. Summary of results
OK, we've successfully fit the model. I could talk more about summarizing the inferences for the 27 items and the 2409 respondents, and about checking the fit using posterior predictive checks, but the focus of today's post is computing.
With computing, then, where are we? What's the takeaway?
• For this example, the model fits just fine using glmer() in the lme4 package.
• lme4 computes the maximum marginal likelihood estimate of the variance parameters, averaging over the regression coefficients. Because this is a multilevel model, it doesn't work to try to maximize the joint likelihood (or find the joint posterior mode); the math on this is in chapter 5 of BDA.
• For this example, the model fails with stan_glmer() in the rstanarm package.
• For this example, the model fits fine in Stan--if you use sum_to_zero_vector.
• When the model isn't fitting well, it makes sense to run with fewer iterations and max_treedepth=5 so that you're not spinning all your cycles for fits that aren't working anyway.
• Despite the above experience for this particular dataset, we can't always recommend lme4, as it has problems when group-level variance parameters are near zero, and it has problems for varying-intercept, varying slope models.
• Surprisingly, Stan converged less well with the normal model than the binomial model.
• We hope that future developments in Stan will make this process easier:
- Nested Laplace should give us the functionality of lmer4 in a more flexible setting, not restricted to the classes of models included in that package and also allowing priors for the variance parameters
- Better adaptation should allow us to reduce the number of default iterations and also avoid the current problem where adaptation goes really slowly for the most poorly-specified models, in violation of the fail fast principle.
- Bob Carpenter told me they have a new variant of Nuts that does some sort of local adaptation which automatically works for the funnel. So then we won't need to choose between the two parameterizations.
10. Other software options
So far, we've tried lme4, rstanarm, and Stan. There are a few more options we can try.
There's INLA, which I think has pretty much the same strengths and weaknesses as lme4 for this problem, so I won't try to figure out how to use it here.
There's fast Nono, which would swallow this problem whole--but I think it only works for normal models, not logistic.
There's brms, which I think has pretty much the same strengths and weaknesses as rstanarm for this problem, so I won't try to figure out how to use it here.
And then there's variational inference. Stan has two variational methods--ADVI and Pathfinder. I'll run them in their default settings from cmdstanr. To stay focused, let's just look at model 3, the parameterization that fit well in Stan:
advi_3 <- park_3$variational(data=stan_data)pathfinder_3 <- park_3$pathfinder(data=stan_data)
ADVI in its default setting takes 4 seconds, Pathfinder takes 70 seconds. They both yield estimates that are in the ballpark, and they both understate uncertainty compared to the model fit in full Stan, which I include below for easy comparison:
> print(advi_3) variable mean median sd mad q5 q95 lp__ -19315.46 -19312.10 59.06 60.49 -19416.52 -19222.58 lp_approx__ -1220.23 -1219.59 35.18 35.89 -1278.46 -1161.80 b[1] -2.70 -2.70 0.01 0.01 -2.72 -2.68 b[2] 0.06 0.06 0.03 0.02 0.02 0.10 b[3] 0.09 0.09 0.06 0.06 -0.01 0.19 b[4] 0.01 0.01 0.00 0.00 0.01 0.02 b[5] 0.00 0.00 0.00 0.00 0.00 0.00 sigma_respondent 2.08 2.08 0.03 0.03 2.03 2.13 sigma_item 2.62 2.57 0.37 0.36 2.07 3.29 a_respondent[1] -0.80 -0.81 0.95 0.99 -2.38 0.82. . .> print(pathfinder_3) variable mean median sd mad q5 q95 lp_approx__ -1250.91 -1250.91 0.00 0.00 -1250.91 -1250.91 lp__ -18120.00 -18120.00 0.00 0.00 -18120.00 -18120.00 b[1] -2.23 -2.23 0.00 0.00 -2.23 -2.23 b[2] 0.07 0.07 0.00 0.00 0.07 0.07 b[3] 0.01 0.01 0.00 0.00 0.01 0.01 b[4] 0.04 0.04 0.00 0.00 0.04 0.04 b[5] 0.01 0.01 0.00 0.00 0.01 0.01 sigma_respondent 1.36 1.36 0.00 0.00 1.36 1.36 sigma_item 2.13 2.13 0.00 0.00 2.13 2.13 a_respondent[1] -0.03 -0.03 0.00 0.00 -0.03 -0.03. . .> print(fit_3) variable mean median sd mad q5 q95 rhat ess_bulk ess_tail lp__ -16714.82 -16714.70 38.92 38.99 -16779.30 -16651.30 1.00 1137 1894 b[1] -2.60 -2.60 0.06 0.06 -2.70 -2.50 1.00 2237 2939 b[2] 0.07 0.07 0.03 0.03 0.02 0.12 1.00 7398 3227 b[3] 0.08 0.08 0.03 0.03 0.03 0.13 1.00 9024 2887 b[4] 0.04 0.04 0.01 0.01 0.03 0.05 1.00 1426 2576 b[5] 0.01 0.01 0.00 0.00 0.01 0.02 1.00 4123 3391 sigma_respondent 1.95 1.95 0.04 0.04 1.89 2.02 1.00 2023 2919 sigma_item 2.48 2.44 0.38 0.36 1.96 3.14 1.00 8438 2806 a_respondent[1] -0.33 -0.28 1.72 1.75 -3.20 2.47 1.00 2998 2964. . .
Actually, Pathfinder shows no uncertainty at all, and it also returns the warning, "Pareto k value (9.2) is greater than 0.7. Importance resampling was not able to improve the approximation, which may indicate that the approximation itself is poor."
ADVI is so fast that maybe it could be good as a starting point for Stan's default NUTS algorithm.
Let's try it! First, Model 1:
advi_1 <- park_1$variational(data=stan_data)fit_after_advi_1 <- park_1$sample(data=stan_data, init=advi_1, parallel_chains=4, max_treedepth=5)print(fit_after_advi_1)
After the usual hundred seconds, here's what we see:
variable mean median sd mad q5 q95 rhat ess_bulk ess_tail lp__ -15074.93 -15074.55 50.84 52.11 -15158.91 -14991.80 1.02 193 436 b[1] -2.54 -2.52 0.46 0.48 -3.35 -1.86 1.40 8 19 b[2] 0.07 0.07 0.03 0.03 0.02 0.13 1.03 335 782 b[3] 0.08 0.08 0.03 0.03 0.03 0.14 1.01 345 569 b[4] 0.04 0.04 0.01 0.01 0.03 0.04 1.04 77 138 b[5] 0.01 0.01 0.00 0.00 0.01 0.02 1.01 594 1121 sigma_respondent 1.96 1.95 0.04 0.04 1.89 2.02 1.02 187 357 sigma_item 2.49 2.41 0.38 0.34 2.01 3.24 1.07 51 107 a_respondent[1] -0.36 -0.26 1.71 1.77 -3.33 2.35 1.01 293 648 a_respondent[2] -0.31 -0.27 0.70 0.69 -1.57 0.75 1.01 388 583. . .
It's not magic--there are still problems with mixing--but it's not bad, either. Similarly when we do with model 2. So for this problem I think that the best option is to run full Stan with max_treedepth=5 and using ADVI as a starting point. Ideally with model 3, but even with one of the poorly-mixing models we still end up with a reasonable answer. It's definitely a better option than running for 8 minutes and still not mixing.
11. Conclusion
It's not always so easy to fit multilevel models. And this model was a pretty easy one! Granted, it had non-nested groupings, but other than that it was simplicity itself: logistic regression with a few predictors and two batches of varying intercepts. For our data and model, lme4 did the job just fine--but we know that in harder problems lme4 can fail. Unfortunately, rstanarm did not work well at all--it was a problem with the parameterization used for the group-level scale parameter. Stan worked, but to avoid it taking too long, we needed a few tricks: (a) use of the right parameterization for those scale parameters, (b) the sum-to-zero constraint on the batches of varying intercepts, (c) setting max_treedepth to a level below its default of 10. Using ADVI as a starting point could make sense too.
This can be taken as a success story (we could fit the model we wanted! using full Bayes! in a reasonable amount of time!) or as a bummer (we needed to work so hard! even for this simple model!).
The next time I work on this sort of problem I'll start with lme4. Often it fails, but when it does work, it's fast, and it's a good place to start. lme4 will rarely be my final step, though, first because I'd like to more fully account for uncertainty, and second because lme4 only works on a limited class of models.
Looking at this problem from an applied perspective, we're coming into the data analysis wanting to estimate ideal points for respondents and items. We'll also want to check the fit of the model and then use it to assess some of the claims made by Dan Luu that got us thinking about this problem in the first place (see the link at the very top of this post). And we'd probably be inclined to elaborate on the model, going far beyond whatever happens to be programmed in lme4, rstanarm, and brms.
It almost makes me want to just give up! But then I remember that all this effort is still easier than the alternative of trying to cobble together a non-model-based data summary. Also the models we're fitting here have the advantage of also working for unbalanced data, which is often an issue in item-response or ideal-point estimation. Finally, doing all the above research should be helpful for me and others working on future problems.
12. How to write this up in a way to be most useful to readers?
When writing up this sort of experience, I'm always torn between making it look clean or showing all the struggles. On one hand, the struggles are important and they give a feel of our workflow. On the other hand, as a reader you could end up getting lost in all the details. I guess the right thing to do is to first present the clean version with the best solution (in this case, that would be lme4), then discuss what to do in harder problems (in this case, just jump to the Stan program that I'm calling Model 3), and only then go back and discuss the full workflow with all the guesses and experimentation.
Perhaps when writing this up more formally I'll do those steps. For now, I'll keep it as is. It already took me many hours to get this far. And I don't think this is the final version. Indeed, I'm hoping that this post will motivate Bob, Charles, and others to put in some improvements to Stan that will allow everything to run much more smoothly! But even after this particular problem gets solved using default software, there will be new problems. The workflow of computation, simulation, and experimentation will continue.
