What day of the year will have the fewest noninduced births? (Difference between mathematical and statistical reasoning)

John Cook points to this charmingly old-school webpage of mathematician Richard Stanley, whose suburban neighbors were Russian spies.

Stanley’s webpage, entitled “Here are a few links not directly related to my research,” is a mix of fun items, boring items, personal links, dead links, something on juggling (I guess you’d expect that from an MIT math professor), and this puzzle:

This one made me happy–it’s a statistics question, and I know the answer! It’s Christmas Day, 25 Dec:

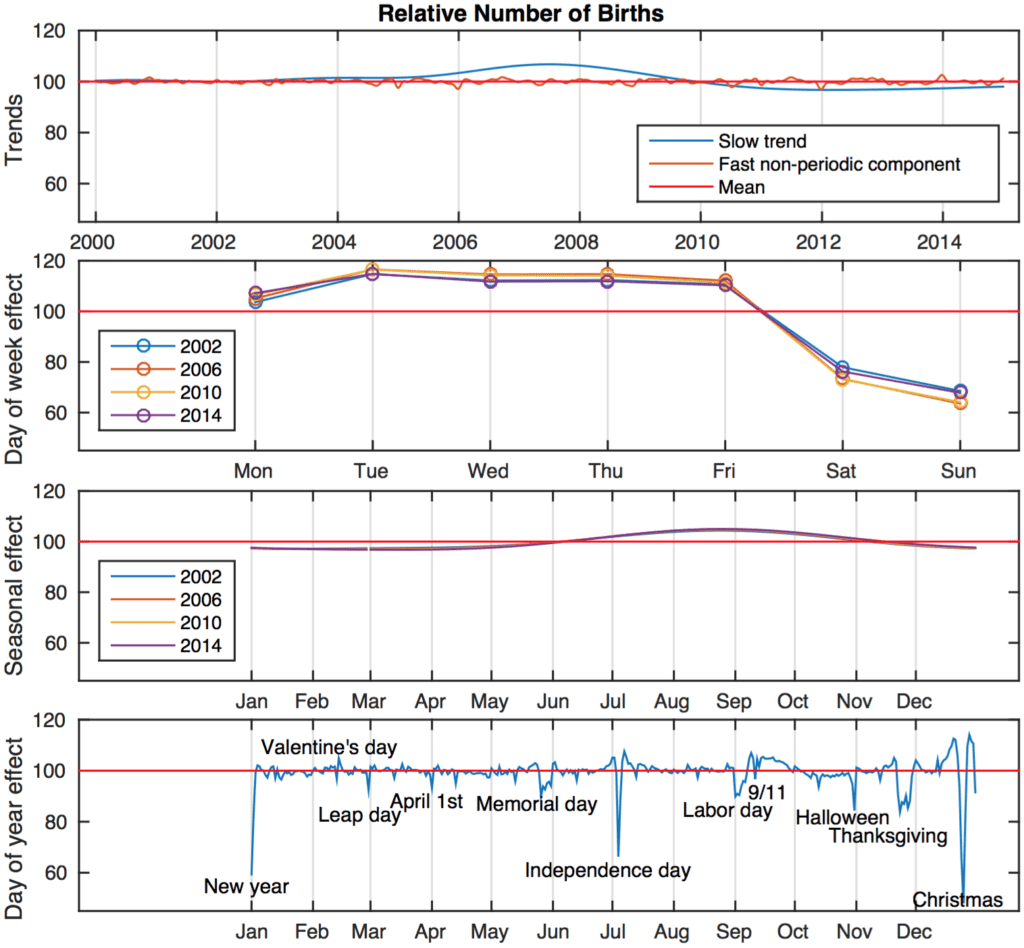
Sure, that’s all births, not just noninduced births–but the pattern for noninduced births has got to be similar. One reason there will be fewer noninduced births on 25 Dec is that a bunch of births were already induced the two days before.

There’s also evidence from this paper on Valentine’s Day and Halloween that spikes in noninduced and induced births go together:

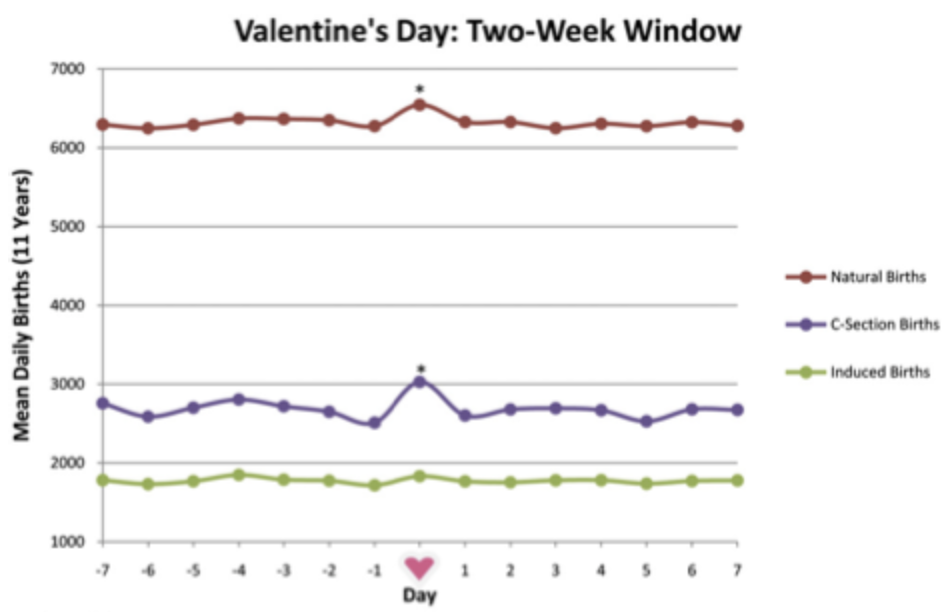
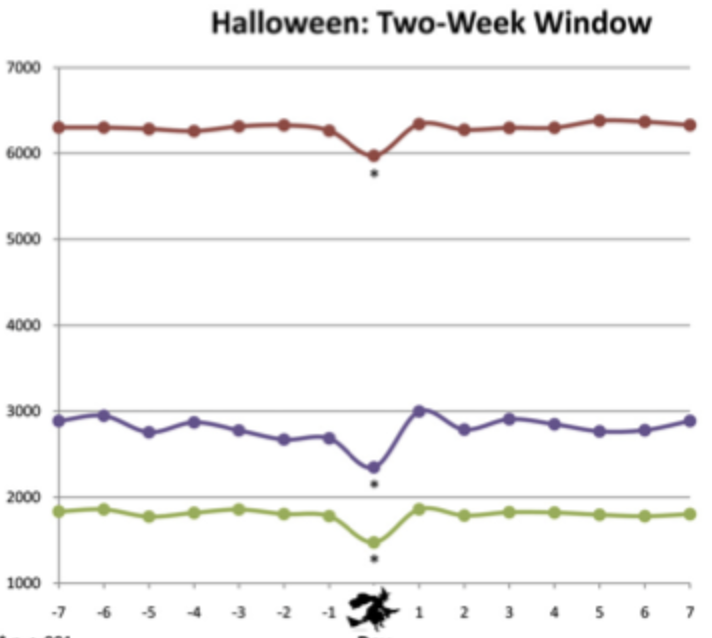
I was curious how Stanley had heard of this–had he read one of our posts on the topic, or maybe he saw it from the graphs on the cover of Bayesian Data Analysis, or maybe this was just some mathematical folklore, or maybe he’d been curious and looked up the numbers himself? I clicked through, and I was surprised to see his answer:

With this elaboration:

That’s a good catch–Aki and I hadn’t thought about that particular issue!–but a factor of 23/24 is pretty small compared to variation between days.

I guess that Stanley’s key mistake was to assume that the noninduced births occur uniformly over time, only varying by season but not by date, day of week, or time of day.

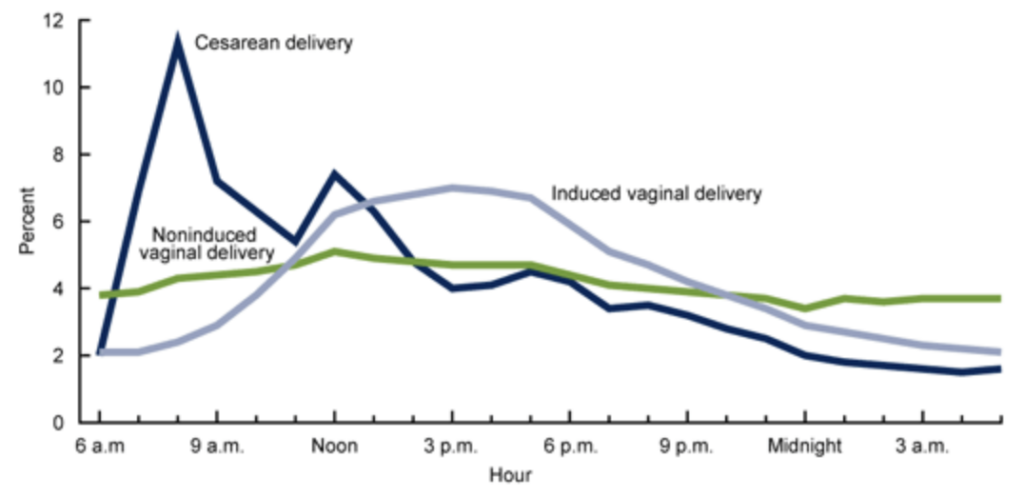
Also, fewer babies are born in the middle of the night:

For lots more information, see this article, “Births and their outcomes by time, day and year: a retrospective birth cohort data linkage study.” It’s from Britain but discusses trends in other countries too.

Anyway, I’m pretty sure that Stanley is mistaken and that 9 Mar is not the day in 2025 that will have the fewest noninduced births.

It’s no big deal–everybody makes mistakes!–but I think it’s a revealing example of the difference between mathematics and statistics.

With mathematics, you start with assumptions–in this case, the assumption that the rate of births varies by season but not by date, day of week, or dime of day–and you use that to derive conclusions. With statistics, you start from the data and work from there.

Neither approach–mathematics or statistics–is always best. It’s good to have both tools. It’s also good to realize which tool is appropriate for which problems.