Chebyshev polynomials as distorted cosines
The Endeavour 2024-08-16
Forman Acton’s book Numerical Methods that Work describes Chebyschev polynomials as
cosine curves with a somewhat disturbed horizontal scale, but the vertical scale has not been touched.
The relation between Chebyshev polynomials and cosines is
Tn(cos θ) = cos(nθ).
Some sources take this as the definition of Chebyshev polynomials. Other sources define the polynomials differently and prove this equation as a theorem.
It follows that if we let x = cos θ then
Tn(x) = cos(n arccos x).
Now sin x = cos(π/2 − x) and for small x, sin x ≈ x. This means
arccos(x) ≈ π/2 − x
for x near 0, and so we should expect the approximation
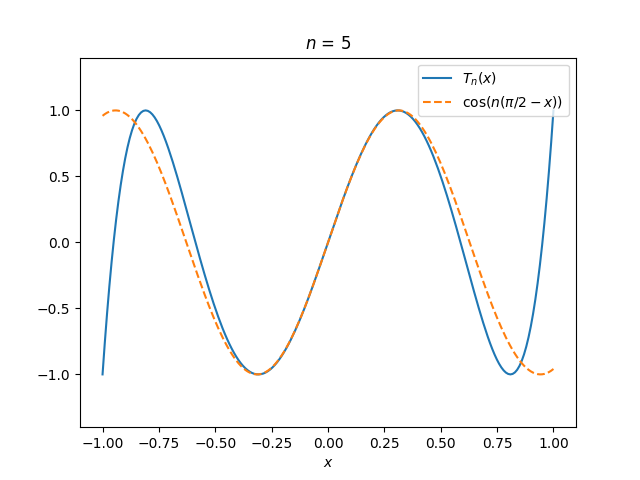
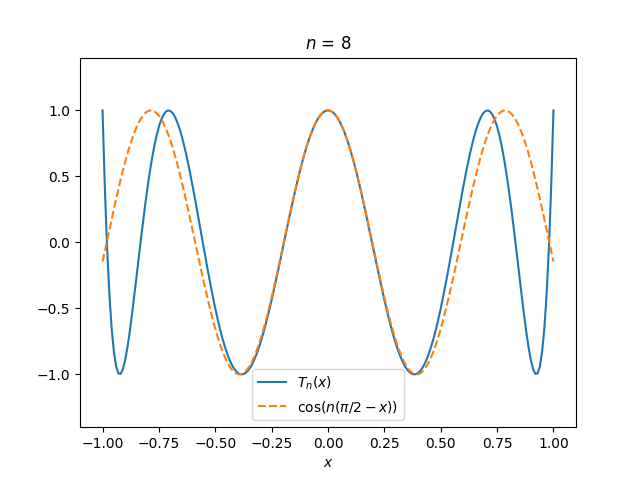
Tn(x) ≈ cos(n(π/2 − x)).
to be accurate near the middle of the interval [−1, 1] though not at the ends. A couple plots show that this is the case.