A couple more variations on an ancient theme
The Endeavour 2024-09-07
I’ve written a couple posts on the approximation
by the Indian astronomer Aryabhata (476–550). The approximation is accurate for x in [−π/2, π/2].
The first post collected a Twitter thread about the approximation into a post. The second looked at how far the coefficients in Aryabhata’s approximation are from the optimal approximation as a ratio of quadratics.
This post will answer a couple questions. First, what value of π did Aryabhata have and how would that effect the approximation error? Second, how bad would Aryabhata’s approximation be if we used the approximation π² ≈ 10?
Using Aryabhata’s value of π
Aryabhata knew the value 3.1416 for π. We know this because he said that a circle of diameter 20,000 would have circumference 62,832. We don’t know, but it’s plausible that he knew π to more accuracy and rounded it to the implied value.
Substituting 3.1416 for π changes the sixth decimal of the approximation, but the approximation is good to only three decimal places, so 3.1416 is as good as a more accurate approximation as far as the error in approximating cosine is concerned.
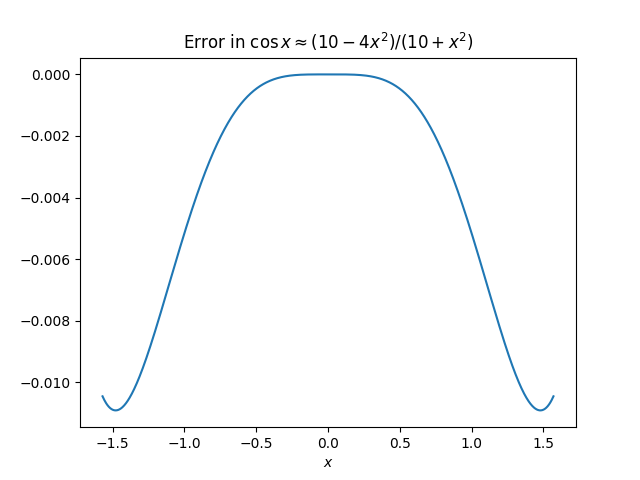
Using π² ≈ 1
Substituting 10 for π² in Aryabhata’s approximation gives an approximation that’s convenient to evaluate by hand.
It’s very accurate for small values of x but the maximum error increases from 0.00163 to 0.01091. Here’s a plot of the error.