Average number of divisors
The Endeavour 2024-10-09
Let d(n) be the number of divisors of an integer n. For example, d(12) = 6 because 12 is divisible by 1, 2, 3, 4, 6, and 12.
The function d varies erratically as the following plot shows.
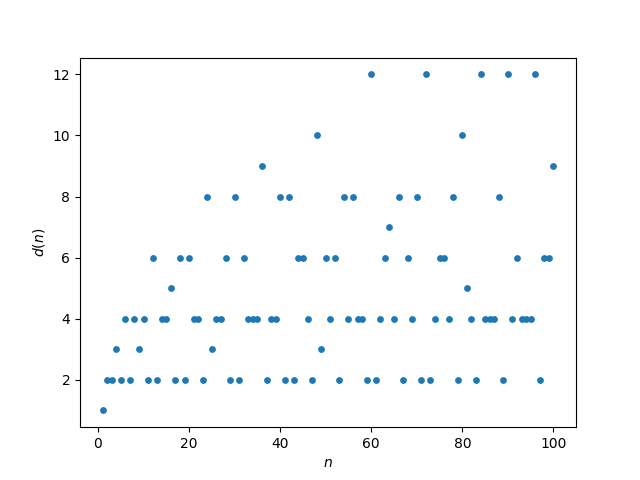
But if you take the running average of d
f(n) = (d(1) + d(2) + d(3) + … + d(n)) / n
then this function is remarkably smoother.

Not only that, the function f(n) converges to log(n).
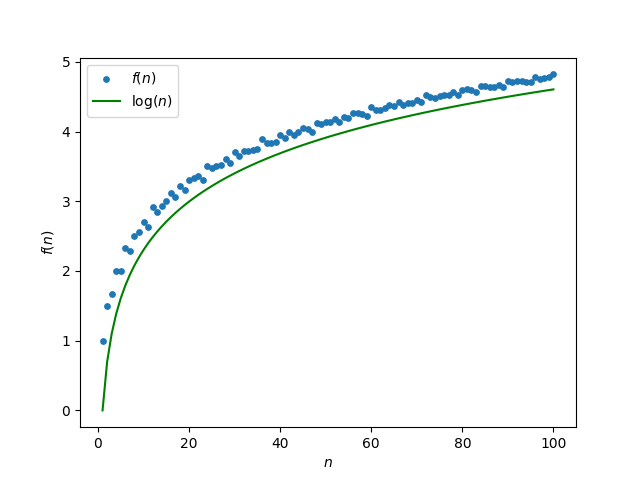
Incidentally, directly computing f(n) for n = 1, 2, 3, …, N would be inefficient because most of the work in computing f(m) would be duplicated in computing f(m + 1). The inefficiency isn’t noticeable for small N but matters more as N increases. It would be more efficient to iteratively compute f(n) by
f(n + 1) = (n f(n) + d(n + 1)) / (n + 1).