Band-limited expansion
The Endeavour 2024-10-28
The band-limited expansion of the function f(x) is given by
where sinc(x) = sin(πx)/πx. This is also called the sinc expansion, or the Whittaker cardinal after its discoverer E. T. Whittaker [1].
This is called the band-limited expansion of f because each term in the infinite sum is band-limited, i.e. only has Fourier spectrum within a finite band, because the Fourier transform of the sinc function is a step function supported between −1/2 and 1/2. [2]
The band-limited expansion has a lot of nice mathematical properties, leading Whittaker to call it “a function of royal blood in the family of entire functions, whose distinguished properties separate it from its bourgeois brethren.”
We can find a band-limited approximation for f by taking only a finite number of terms in the sum. An advantage of the band-limited approximation over a truncated Fourier series is that the former converges faster, making it useful in numerical algorithms [3]. Here’s an example of approximating the function exp(−x²) by taking h = 1 and using three terms, i.e. k running from −1 to 1.
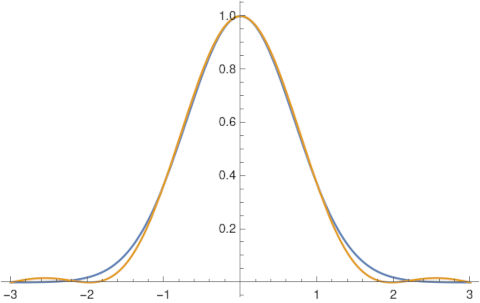
You can improve the accuracy of the approximation by decreasing the size of h or by increasing N. This post explains how to pick the trade-off between h and N to minimize approximation error.
Related posts
[1] E. T. Whittaker, On the functions which are represented by the expansions of the interpolation theory, Proc. Roy. Soc. Edinburgh, 35 (1915), pp. 181–194.
[2] You may get a different interval of support if you use a different convention for defining the Fourier transform. Unfortunately there are many conventions.
[3] Frank Stenger. Numerical Methods based on Whittaker Cardinal, or Sinc Functions. Source: SIAM Review, Apr., 1981, Vol. 23, No. 2 (Apr., 1981), pp. 165-224
The post Band-limited expansion first appeared on John D. Cook.