Trying to fit a logistic curve
The Endeavour 2025-12-20
A logistic curve, sometimes called an S curve, looks different in different regions. Like the proverbial blind men feeling different parts of an elephant, people looking at different segments of the curve could come to very different impressions of the full picture. 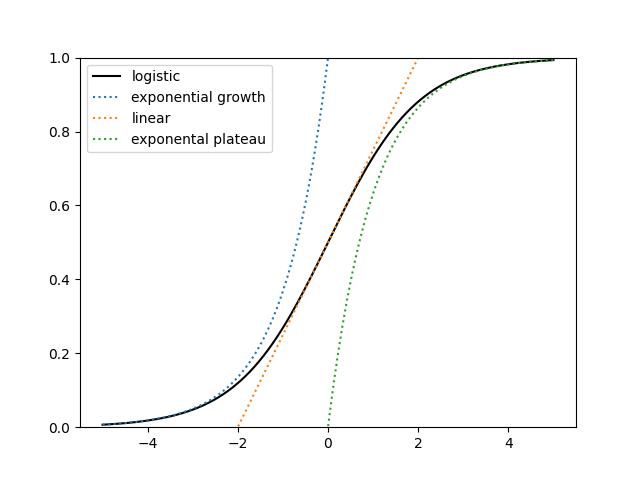
It’s naive to look at the left end and assume the curve will grow exponentially forever, even if the data are statistically indistinguishable from exponential growth.
A slightly less naive approach is to look at the left end, assume logistic growth, and try to infer the parameters of the logistic curve. In the image above, you may be able to forecast the asymptotic value if you have data up to time t = 2, but it would be hopeless to do so with only data up to time t = −2. (This post was motivated by seeing someone trying to extrapolate a logistic curve from just its left tail.)
Suppose you know with absolute certainty that your data have the form
where ε is some small amount of measurement error. The world is not obligated follow a simple mathematical model, or any mathematical model for that matter, but for this post we will assume that for some inexplicable reason you know the future follows a logistic curve; the only question is what the parameters are.
Furthermore, we only care about fitting the a parameter. That is, we only want to predict the asymptotic value of the curve. This is easier than trying to fit the b or c parameters.
Simulation experiment
I generated 16 random t values between −5 and −2, plugged them into the logistic function with parameters a = 1, b = 1, and c = 0, then added Gaussian noise with standard deviation 0.05.
My intention was to do this 1000 times and report the range of fitted values for a. However, the software I was using (scipy.optimize.curve_fit) failed to converge. Instead it returned the following error message.
RuntimeError: Optimal parameters not found: Number of calls to function has reached maxfev = 800.
When you see a message like that, your first response is probably to tweak the code so that it converges. Sometimes that’s the right thing to do, but often such numerical difficulties are trying to tell you that you’re solving the wrong problem.
When I generated points between −5 and 0, the curve_fit algorithm still failed to converge.
When I generated points between −5 and 2, the fitting algorithm converged. The range of a values was from 0.8254 to 1.6965.
When I generated points between −5 and 3, the range of a values was from 0.9039 to 1.1815.
Increasing the number of generated points did not change whether the curve fitting method converge, though it did result in a smaller range of fitted parameter values when it did converge.
I said we’re only interested in fitting the a parameter. I looked at the ranges of the other parameters as well, and as expected, they had a wider range of values.
So in summary, fitting a logistic curve with data only on the left side of the curve, to the left of the inflection point in the middle, may completely fail or give you results with wide error estimates. And it’s better to have a few points spread out through the domain of the function than to have a large number of points only on one end.
Related posts
- Logistic regression quick takes
- Laplace approximation for Bayesian logistic regression
- Fixed points of logistic function