Perfect and imperfect shuffles

Take a deck of cards and cut it in half, placing the top half of the deck in one hand and the bottom half in the other. Now bend the stack of cards in each hand and let cards alternately fall from each hand. This is called a rifle shuffle.

Random shuffles

Persi Diaconis proved that it takes seven shuffles to fully randomize a desk of 52 cards. He studied videos of people shuffling cards in order to construct a realistic model of the shuffling process.

Shuffling randomizes a deck of cards due to imperfections in the process. You may not cut the deck exactly in half, and you don’t exactly interleave the two halves of the deck. Maybe one card falls from your left hand, then two from your right, etc.

Diaconis modeled the process with a probability distribution on how many cards are likely to fall each time. And because his model was realistic, after seven shuffles a deck really is well randomized.

Perfect shuffles

Now suppose we take the imperfection out of shuffling. We do cut the deck of cards exactly in half each time, and we let exactly one card fall from each half each time. And to be specific, let’s say the first card will always fall from the top half of the deck. That is, we do an in-shuffle [1]. A perfect in-shuffle does not randomize a deck because it’s a deterministic permutation.

To illustrate a perfect in-shuffle, suppose you start with a deck of these six cards.

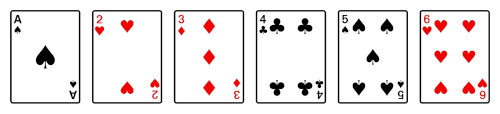
Then you divide the deck into two halves.

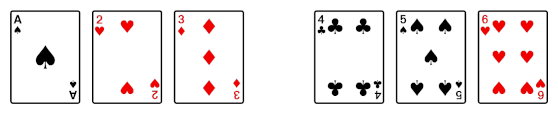
Then after the shuffle you have the following.

Incidentally, I created the images above using a font that included glyphs for the Unicode characters for playing cards. More on that here. The font produced black-and-white images, so I edited the output in GIMP to turn things red that should be red.

Coming full circle

If you do enough perfect shuffles, the deck returns to its original order. This could be the basis for a magic trick, if the magician has the skill to repeatedly perform a perfect shuffle.

Performing k perfect in-shuffles will restore the order of a deck of n cards if

2^k = 1 (mod n + 1).

So, for example, after 52 in-shuffles, a deck of 52 cards returns to its original order. We can see this from a quick calculation at the Python REPL:

>>> 2**52 % 531

With slightly more work we can show that less than 52 shuffles won’t do.

>>> for k in range(1, 53):    ... if 2**k % 53 == 1: print(k)52

The minimum number of shuffles is not always the same as the size of the deck. For example, it takes 4 shuffles to restore the order of a desk of 14 cards.

>>> 2**4 % 151

Shuffle code

Here’s a function to perform a perfect in-shuffle.

def shuffle(deck):    n = len(deck)    return [item for pair in zip(deck[n//2 :], deck[:n//2]) for item in pair]

With this you can confirm the results above. For example,

n = 14k = 4deck = list(range(n))for _ in range(k):    deck = shuffle(deck)print(deck)

This prints 0, 1, 2, …, 13 as expected.

Related posts

• Distribution of matches between two decks
• Shuffle product
• Random walk on a circle

[2] If the first card falls from the bottom half, that’s called an out-shuffle. In that case the bottom card remains on bottom, and the top card remains on top. If you swap the order of the two arguments to zip above, the shuffle function will perform an out-shuffle. Performing k perfect out-shuffles will restore the order of a deck of n cards if

2^k = 1 (mod n − 1).

So for a deck of 52 cards, 8 out-shuffles will return the deck to its original order.

The post Perfect and imperfect shuffles first appeared on John D. Cook.