Bounding the perimeter of a triangle between circles

Suppose you have a triangle and you know the size of the largest circle that can fit inside (the incircle) and the size of the smallest circle that can fit outside (the circumcircle). How would you estimate the perimeter of the triangle?

In terms of the figure below, if you know the circumference of the red and blue circles, how could you estimate the perimeter of the black triangle?

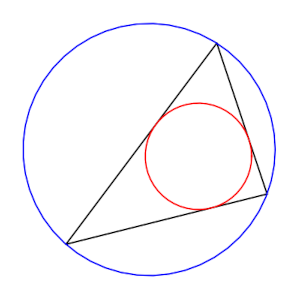
A crude estimate is that the triangle perimeter must be greater than the incircle circumference and less than the circumcircle circumference. But we can do better.

Here I will present Gerretsen’s inequalities, but there are other approaches that give tighter bounds for some triangles.

It is conventional in this kind of problem to work with the semiperimeter of the triangle, half the perimeter, rather than the perimeter. Let r be the radius of the incircle, R the radius of the circumcircle, and s the semiperimeter of the triangle. Then Gerretsen’s inequalities say

16Rr − 5r² ≤ s² ≤ 4R² + 4Rr + 3r²

In the figure above,

r = 1.058, R = 2.5074, s = 6.1427

and Gerretsen’s inequalities give

36.8532  ≤ s² = 37.7327 ≤ 39.1200.

In the case of an equilateral triangle, Gerretsen’s inequalities are in fact equalities:

16Rr − 5r² = s² = 4R² + 4Rr + 3r².

Related posts

• Johnson’s circle theorem
• Nine-point circle theorem
• Euler line

[1] J. C. H. Gerretsen, Ongelijkheden in de driehoek. Nieuw Tijdschr 41 (1953), 1–7.

The post Bounding the perimeter of a triangle between circles first appeared on John D. Cook.