Subtraction Is Crazy

I was re-reading Michael Murray’s explanation of cointegration:

and marvelling at calculus.

Calculus blows my mind sometimes. Like, hey guess how much we can do with subtraction.

— protëa(@isomorphisms) March 28, 2013

Of course it’s not any subtraction. It’s subtracting a function from a shifted version of itself. Still doesn’t sound like a universal revolution.

(But of course the observation that the lagged first-difference will be zero around an extremum (turning point), along with analytic methods of calculating the (infinitesimal) first-differences of a function, made a pretty big splash.)

Jeff Ryan wrote some R functions that make it very easy to first-difference financial time series.

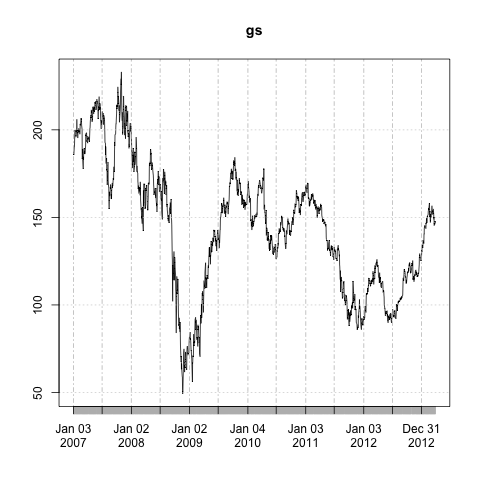
Here’s how to do the first differences of Goldman Sachs’ share price:

require(quantmod)getSymbols("GS")gs <- Ad(GS)plot(  gs - lag(gs)  )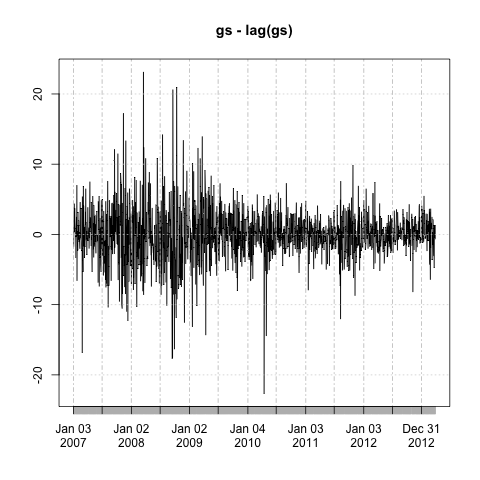

Look how much more structured the result is! Now all of the numbers are within a fairly narrow band. With length(gs) I found 1570 observations. Here are 1570 random normals plot(rnorm(1570, sd=10), type="l") for comparison:

Not perfectly similar, but very close!

Looking at the first differences compared to a Gaussian is also a nifty way to show what’s different between public equity markets and a random walk. What most obviously sticks out to me is the vol going up periodically in the $GS time series.

I think I got even a little closer with drawing the stdev’s from a Poisson process plot(rnorm(1570, sd=rpois(1570, lambda=5)), type="l")

but I’ll end there with the graphical futzing.

What’s really amazing to me is how much difference a subtraction makes.