We really should set aside more time for cool math

One of the disadvantages of having so much to talk about (literally thousands of items in the draft folder waiting for completion) is that so much fun stuff gets pushed aside. Case in point: this post from John D. Cook.

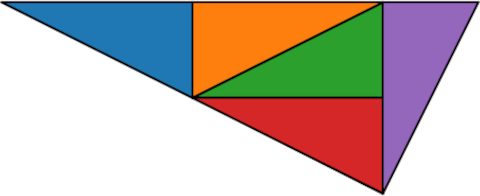
John Conway discovered a right triangle that can be partitioned into five similar triangles. The sides are in proportion 1 : 2 : √5.

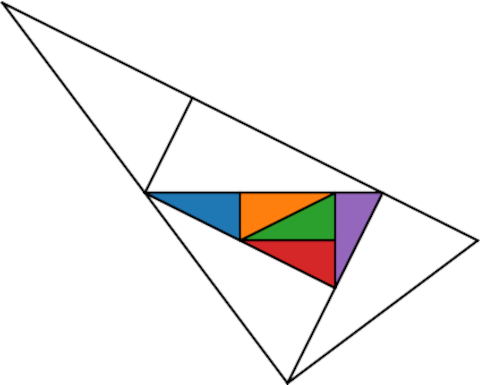
You can make a larger similar triangle by making the entire triangle the central (green) triangle of a new triangle.

Cook later points out that repeating this gives us an aperiodic tiling of the plane and has a cool animation. 

 If I were still teaching high school geometry (and wasn't being Common-Cored into submission), I'd make the following assignment.

Prove these five smaller triangles are similar to the large one.

Prove these five smaller triangles are congruent to each other.

Find the ratio of the corresponding sides of the small triangles to the corresponding sides of the large triangle. 

Prove that this partitioning of a right triangle would only work for sides in proportion 1 : 2 : √5..