Higher uniformity of arithmetic functions in short intervals II. Almost all intervals

What's new 2024-11-11

Kaisa Matomäki, Maksym Radziwill, Fernando Xuancheng Shao, Joni Teräväinen, and myself have (finally) uploaded to the arXiv our paper “Higher uniformity of arithmetic functions in short intervals II. Almost all intervals“. This is a sequel to our previous paper from 2022. In that paper, discorrelation estimates such as

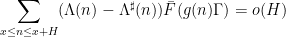
$\displaystyle \sum_{x \leq n \leq x+H} (\Lambda(n) - \Lambda^\sharp(n)) \bar{F}(g(n)\Gamma) = o(H)$

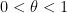
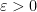
were established, where ${\Lambda}$ is the von Mangoldt function, ${\Lambda^\sharp}$ was some suitable approximant to that function, ${F(g(n)\Gamma)}$ was a nilsequence, and ${[x,x+H]}$ was a reasonably short interval in the sense that ${H \sim x^{\theta+\varepsilon}}$ for some ${0 < \theta < 1}$ and some small ${\varepsilon>0}$ . 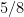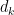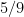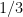In that paper, we were able to obtain non-trivial estimates for ${\theta}$ as small as ${5/8}$ , and for some other functions such as divisor functions ${d_k}$ for small values of ${k}$ , we could lower ${\theta}$ somewhat to values such as ${3/5}$ , ${5/9}$ , ${1/3}$ of ${\theta}$ . This had a number of analytic number theory consequences, for instance in obtaining asymptotics for additive patterns in primes in such intervals. However, there were multiple obstructions to lowering ${\theta}$ much further. 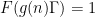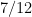Even for the model problem when ${F(g(n)\Gamma) = 1}$ , that is to say the study of primes in short intervals, until recently the best value of ${\theta}$ available was ${7/12}$ , although this was very recently improved to ${17/30}$ by Guth and Maynard.

However, the situation is better when one is willing to consider estimates that are valid for almost all intervals, rather than all intervals, so that one now studies local higher order uniformity estimates of the form

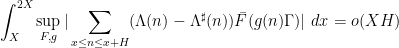
$\displaystyle \int_X^{2X} \sup_{F,g} | \sum_{x \leq n \leq x+H} (\Lambda(n) - \Lambda^\sharp(n)) \bar{F}(g(n)\Gamma)|\ dx = o(XH)$

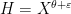
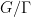
where ${H = X^{\theta+\varepsilon}}$ and the supremum is over all nilsequences of a certain Lipschitz constant on a fixed nilmanifold ${G/\Gamma}$ . This generalizes local Fourier uniformity estimates of the form

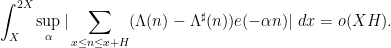
$\displaystyle \int_X^{2X} \sup_{\alpha} | \sum_{x \leq n \leq x+H} (\Lambda(n) - \Lambda^\sharp(n)) e(-\alpha n)|\ dx = o(XH).$

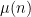
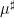
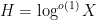
There is particular interest in such estimates in the case of the Möbius function ${\mu(n)}$ (where, as per the Möbius pseudorandomness conjecture, the approximant ${\mu^\sharp}$ should be taken to be zero, at least in the absence of a Siegel zero). This is because if one could get estimates of this form for any ${H}$ that grows sufficiently slowly in ${X}$ (in particular ${H = \log^{o(1)} X}$ ), this would imply the (logarithmically averaged) Chowla conjecture, as I showed in a previous paper.

While one can lower ${\theta}$ somewhat, there are still barriers. For instance, in the model case ${F \equiv 1}$ , that is to say prime number theorems in almost all short intervals, until very recently the best value of ${\theta}$ was ${1/6}$ , recently lowered to ${2/15}$ by Guth and Maynard (and can be lowered all the way to zero on the Density Hypothesis). Nevertheless, we are able to get some improvements at higher orders:

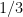For the von Mangoldt function, we can get ${\theta}$ as low as ${1/3}$ , with an arbitrary logarithmic saving ${\log^{-A} X}$ in the error terms; for divisor functions, one can even get power savings in this regime.
For the Möbius function, we can get 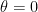${\theta=0}$ , recovering our previous result with Tamar Ziegler, but now with ${\log^{-A} X}$ type savings in the exceptional set (though not in the pointwise bound outside of the set).
We can now also get comparable results for the divisor function.

As sample applications, we can obtain Hardy-Littlewood conjecture asymptotics for arithmetic progressions of almost all given steps ${h \sim X^{1/3+\varepsilon}}$ , and divisor correlation estimates on arithmetic progressions for almost all ${h \sim X^\varepsilon}$ .

Our proofs are rather long, but broadly follow the “contagion” strategy of Walsh, generalized from the Fourier setting to the higher order setting. Firstly, by standard Heath–Brown type decompositions, and previous results, it suffices to control “Type II” discorrelations such as

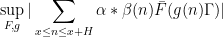
$\displaystyle \sup_{F,g} | \sum_{x \leq n \leq x+H} \alpha*\beta(n) \bar{F}(g(n)\Gamma)|$

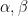
for almost all ${x}$ , and some suitable functions ${\alpha,\beta}$ supported on medium scales. So the bad case is when for most ${x}$ , one has a discorrelation

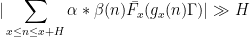
$\displaystyle |\sum_{x \leq n \leq x+H} \alpha*\beta(n) \bar{F_x}(g_x(n)\Gamma)| \gg H$

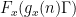
for some nilsequence ${F_x(g_x(n) \Gamma)}$ that depends on ${x}$ .

The main issue is the dependency of the polynomial ${g_x}$ on ${x}$ . By using a “nilsequence large sieve” introduced in our previous paper, and removing degenerate cases, we can show a functional relationship amongst the ${g_x}$ that is very roughly of the form

$\displaystyle g_x(an) \approx g_{x'}(a'n)$

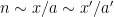
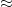
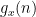
whenever ${n \sim x/a \sim x'/a'}$ (and I am being extremely vague as to what the relation “ ${\approx}$ ” means here). 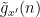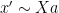By a higher order (and quantitatively stronger) version of Walsh’s contagion analysis (which is ultimately to do with separation properties of Farey sequences), we can show that this implies that these polynomials ${g_x(n)}$ (which exert influence over intervals ${[x,x+H]}$ ) can “infect” longer intervals ${[x', x'+Ha]}$ with some new polynomials ${\tilde g_{x'}(n)}$ and various ${x' \sim Xa}$ , which are related to many of the previous polynomials by a relationship that looks very roughly like

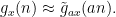
$\displaystyle g_x(n) \approx \tilde g_{ax}(an).$

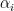
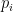
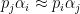
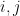
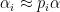
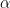
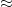
This can be viewed as a rather complicated generalization of the following vaguely “cohomological”-looking observation: if one has some real numbers ${\alpha_i}$ and some primes ${p_i}$ with ${p_j \alpha_i \approx p_i \alpha_j}$ for all ${i,j}$ , then one should have ${\alpha_i \approx p_i \alpha}$ for some ${\alpha}$ , where I am being vague here about what ${\approx}$ means (and why it might be useful to have primes). 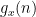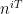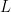By iterating this sort of contagion relationship, one can eventually get the ${g_x(n)}$ to behave like an Archimedean character ${n^{iT}}$ for some ${T}$ that is not too large (polynomial size in ${X}$ ), and then one can use relatively standard (but technically a bit lengthy) “major arc” techiques based on various integral estimates for zeta and ${L}$ functions to conclude.