Quantitative correlations and some problems on prime factors of consecutive integers

What's new 2025-12-02

Joni Teravainen and I have uploaded to the arXiv my paper “Quantitative correlations and some problems on prime factors of consecutive integers“. This paper applies modern analytic number theory tools – most notably, the Maynard sieve and the recent correlation estimates for bounded multiplicative functions of Pilatte – to resolve (either partially or fully) some old problems of Erdős, Strauss, Pomerance, Sárközy, and Hildebrand, mostly regarding the prime counting function

$\displaystyle \omega(n) := \sum_{p|n} 1$

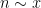
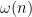
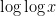
and its relatives. The famous Hardy–Ramanujan and Erdős–Kac laws tell us that asymptotically for ${n \sim x}$ , ${\omega(n)}$ should behave like a gaussian random variable with mean and variance both close to ${\log\log x}$ ; but the question of the joint distribution of consecutive values such as ${\omega(n), \omega(n+1)}$ is still only partially understood. 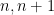Aside from some lower order correlations at small primes (arising from such observations as the fact that precisely one of ${n,n+1}$ will be divisible by ${2}$ ), the expectation is that such consecutive values behave like independent random variables. 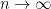As an indication of the state of the art, it was recently shown by Charamaras and Richter that any bounded observables ${f(\omega(n))}$ , ${g(\omega(n+1))}$ will be asymptotically decorrelated in the limit ${n \rightarrow \infty}$ if one performs a logarithmic statistical averaging. Roughly speaking, this confirms the independence heuristic at the scale ${\sqrt{\log\log x}}$ of the standard deviation, but does not resolve finer-grained information, such as precisely estimating the probability of the event ${\omega(n)=\omega(n+1)}$ .

Our first result, answering a question of Erdős, shows that there are infinitely many ${n}$ for which one has the bound

$\displaystyle \omega(n+k) \ll k$

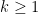
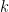
for all ${k \geq 1}$ . For ${k \gg \log\log n}$ , such a bound is already to be expected (though not completely universal) from the Hardy–Ramanujan law; the main difficulty is thus with the short shifts ${k = o(\log\log n)}$ . If one only had to demonstrate this type of bound for a bounded number of ${k}$ , then this type of result is well within standard sieve theory methods, which can make any bounded number of shifts ${n+k}$ “almost prime” in the sense that ${\omega(n+k)}$ becomes bounded. Thus the problem is that the “sieve dimension” ${\sim \log\log n}$ grows (slowly) with ${n}$ . When writing about this problem in 1980, Erdős and Graham write “we just know too little about sieves to be able to handle such a question (“we” here means not just us but the collective wisdom (?) of our poor struggling human race)”.

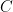However, with the advent of the Maynard sieve (also sometimes referred to as the Maynard–Tao sieve), it turns out to be possible to sieve for the conditions ${\omega(n+k) \ll k}$ for all ${k = o(\log\log n)}$ simultaneously (roughly speaking, by sieving out any ${n}$ for which ${n+k}$ is divisible by a prime ${p \ll x^{1/\exp(Ck)}}$ for a large ${C}$ ), and then performing a moment calculation analogous to the standard proof (due to Turán) of the Hardy–Ramanujan law, but weighted by the Maynard sieve. (In order to get good enough convergence, one needs to control fourth moments as well as second moments, but these are standard, if somewhat tedious, calculations).

Our second result, which answers a separate question of Erdős, establishes that the quantity

$\displaystyle \sum_n \frac{\omega(n)}{2^n} = 0.5169428\dots$

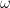
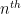
is irrational; this had recently been established by Platt under the assumption of the prime tuples conjecture, but we are able to establish this result unconditoinally. 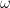The binary expansion of this number is of course closely related to the distribution of ${\omega}$ , but in view of the Hardy–Ramanujan law, the ${n^{th}}$ digit of this number is influenced by about ${\log\log\log n}$ nearby values of ${\omega}$ , which is too many correlations for current technology to handle. However, it is possible to do some “Gowers norm” type calculations to decouple things to the point where pairwise correlation information is sufficient. 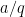To see this, suppose for contradiction that this number was a rational ${a/q}$ , thus

$\displaystyle q \sum_n \frac{\omega(n)}{2^n} = 0 \hbox{ mod } 1.$

Multiplying by ${2^n}$ , we obtain some relations between shifts ${\omega(n+h)}$ :

$\displaystyle q \sum_{h=1}^\infty \frac{\omega(n+h)}{2^h} = 0 \hbox{ mod } 1.$

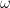
Using the additive nature of ${\omega}$ , one then also gets similar relations on arithmetic progressions, for many ${n}$ and ${p}$ :

$\displaystyle q \sum_{h=1}^\infty \frac{\omega(n+ph)}{2^h} = 0 \hbox{ mod } 1.$

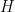
Taking alternating sums of this sort of identity for various ${n}$ and ${p}$ (in analogy to how averages involving arithmetic progressions can be related to Gowers norm-type expressions over cubes), one can eventually arrive eliminate the contribution of small ${H}$ , and arrive at an identity of the form

$\displaystyle q \sum_{h=1}^\infty \frac{\sum_{\epsilon \in \{0,1\}^K} (-1)^{|\epsilon|} \omega(n + r_{\epsilon,h+K})}{2^{h+K}} = 0 \hbox{ mod } 1 \ \ \ \ \ (1)$

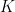
for many ${n}$ , where ${K}$ is a parameter (we eventually take ${K \sim \log\log\log\log n}$ ) and ${r_{\epsilon,h+K}}$ are various shifts that we will not write out explicitly here. This looks like quite a messy expression; however, one can adapt proofs of the Erdős–Kac law and show that, as long as one ignores the contribution of really large prime factors (of order ${\gg n^{1/10}}$ , say) to the ${\omega(n + r_{\epsilon,h+K})}$ , that this sort of sum behaves like a gaussian, and in particular once one can show a suitable local limit theorem, one can contradict (1). 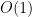The contribution of the large prime factors does cause a problem though, as a naive application of the triangle inequality bounds this contribution by ${O(1)}$ , which is an error that overwhelms the information provided by (1). To resolve this we have to adapt the pairwise correlation estimates of Pilatte mentioned earlier to demonstrate that the these contributions are in fact ${o(1)}$ . 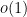Here it is important that the error estimates of Pilatte are quite strong (of order ${O(\log^{-c} n)}$ ); previous correlation estimates of this type (such as those used in this earlier paper with Joni) turn out to be too weak for this argument to close.

Our final result concerns the asymptotic behavior of the density

$\displaystyle \frac{1}{x} \{n \leq x: \omega(n+1) = \omega(n)\}$

(we also address similar questions for ${\Omega(n+1)=\Omega(n)}$ and ${\tau(n+1)=\tau(n)}$ ). Heuristic arguments led Erdős, Pomerance, and Sárközy to conjecture that this quantity was asymptotically ${\frac{1}{2\sqrt{\pi \log\log x}}}$ . They were able to establish an upper bound of ${O(1/\log\log x)}$ , while Hildebrand obtained a lower bound of ${\gg 1/(\log\log x)^3}$ , due to Hildebrand. Here, we obtain the asymptotic for almost all ${x}$ (the limitation here is the standard one, which is that the current technology on pairwise correlation estimates either requires logarithmic averaging, or is restricted to almost all scales rather than all scales). Roughly speaking, the idea is to use the circle method to rewrite the above density in terms of expressions

$\displaystyle \frac{1}{x} \sum_{n \leq x} e(\alpha \omega(n+1)) e(-\alpha \omega(n))$

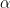
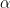
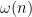
for various frequencies ${\alpha}$ , use the estimates of Pilatte to handle the minor arc ${\alpha}$ , and convert the major arc contribution back into physical space (in which ${\omega(n+1)}$ and ${\omega(n)}$ are now permitted to differ by a large amount) and use more traditional sieve theoretic methods to estimate the result.