Monotone non-decreasing sequences of the Euler totient function

What's new 2023-09-06

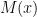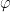I have just uploaded to the arXiv my paper “Monotone non-decreasing sequences of the Euler totient function“. This paper concerns the quantity ${M(x)}$ , defined as the length of the longest subsequence of the numbers from ${1}$ to ${x}$ for which the Euler totient function ${\varphi}$ is non-decreasing. The first few values of 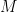${M}$ are

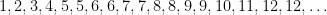
$\displaystyle 1, 2, 3, 4, 5, 5, 6, 6, 7, 7, 8, 8, 9, 9, 10, 11, 12, 12, \dots$

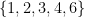
(OEIS A365339). For instance, ${M(6)=5}$ because the totient function is non-decreasing on the set ${\{1,2,3,4,5\}}$ or ${\{1,2,3,4,6\}}$ , but not on the set ${\{1,2,3,4,5,6\}}$ .

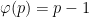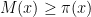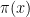Since ${\varphi(p)=p-1}$ for any prime ${p}$ , we have ${M(x) \geq \pi(x)}$ , where ${\pi(x)}$ is the prime counting function. Empirically, the primes come quite close to achieving the maximum length 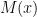${M(x)}$ ; indeed it was conjectured by Pollack, Pomerance, and Treviño, based on numerical evidence, that one had

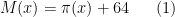
$\displaystyle M(x) = \pi(x)+64 \ \ \ \ \ (1)$

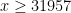
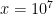
for all ${x \geq 31957}$ ; this conjecture is verified up to ${x=10^7}$ . The previous best known upper bound was basically of the form

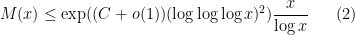
$\displaystyle M(x) \leq \exp( (C+o(1)) (\log\log\log x)^2 ) \frac{x}{\log x} \ \ \ \ \ (2)$

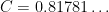
as ${x \rightarrow \infty}$ for an explicit constant ${C = 0.81781\dots}$ , from combining results from the above paper with that of Ford or of Maier-Pomerance. In this paper we obtain the asymptotic

$\displaystyle M(x) = \left( 1 + O \left(\frac{(\log\log x)^5}{\log x}\right) \right) \frac{x}{\log x}$

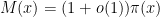
so in particular ${M(x) = (1+o(1))\pi(x)}$ . This answers a question of Erdős, as well as a closely related question of Pollack, Pomerance, and Treviño.

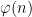The methods of proof turn out to be mostly elementary (the most advanced result from analytic number theory we need is the prime number theorem with classical error term). The basic idea is to isolate one key prime factor ${p}$ of a given number ${1 \leq n \leq x}$ which has a sizeable influence on the totient function ${\varphi(n)}$ . For instance, for “typical” numbers ${n}$ , one has a factorization

$\displaystyle n = d p_2 p_1$

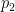
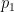
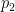
where ${p_2}$ is a medium sized prime, ${p_1}$ is a significantly larger prime, and ${d}$ is a number with all prime factors less than ${p_2}$ . This leads to an approximation

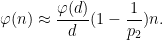
$\displaystyle \varphi(n) \approx \frac{\varphi(d)}{d} (1-\frac{1}{p_2}) n.$

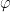
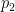
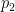
As a consequence, if we temporarily hold ${d}$ fixed, and also localize ${n}$ to a relatively short interval, then ${\varphi}$ can only be non-decreasing in ${n}$ if ${p_2}$ is also non-decreasing at the same time. 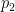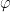This turns out to significantly cut down on the possible length of a non-decreasing sequence in this regime, particularly if ${p_2}$ is large; this can be formalized by partitioning the range of ${p_2}$ into various subintervals and inspecting how this (and the monotonicity hypothesis on ${\varphi}$ ) constrains the values of ${n}$ associated to each subinterval. 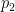When ${p_2}$ is small, we instead use a factorization

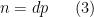
$\displaystyle n = d p \ \ \ \ \ (3)$

where ${d}$ is very smooth (i.e., has no large prime factors), and ${p}$ is a large prime. Now we have the approximation

$\displaystyle \varphi(n) \approx \frac{\varphi(d)}{d} n \ \ \ \ \ (4)$

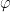
and we can conclude that ${\frac{\varphi(d)}{d}}$ will have to basically be piecewise constant in order for ${\varphi}$ to be non-decreasing. Pursuing this analysis more carefully (in particular controlling the size of various exceptional sets in which the above analysis breaks down), we end up achieving the main theorem so long as we can prove the preliminary inequality

$\displaystyle \sum_{\frac{\varphi(d)}{d}=q} \frac{1}{d} \leq 1 \ \ \ \ \ (5)$

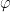
for all positive rational numbers ${q}$ . This is in fact also a necessary condition; any failure of this inequality can be easily converted to a counterexample to the bound (2), by considering numbers of the form (3) with ${\frac{\varphi(d)}{d}}$ equal to a fixed constant ${q}$ (and omitting a few rare values of ${n}$ where the approximation (4) is bad enough that ${\varphi}$ is temporarily decreasing). 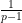Fortunately, there is a minor miracle, relating to the fact that the largest prime factor of denominator of ${\frac{\varphi(d)}{d}}$ in lowest terms necessarily equals the largest prime factor of ${d}$ , that allows one to evaluate the left-hand side of (5) almost exactly (this expression either vanishes, or is the product of ${\frac{1}{p-1}}$ for some primes ${p}$ ranging up to the largest prime factor of ${q}$ ) that allows one to easily establish (5). If one were to try to prove an analogue of our main result for the sum-of-divisors function 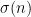${\sigma(n)}$ , one would need the analogue

$\displaystyle \sum_{\frac{\sigma(d)}{d}=q} \frac{1}{d} \leq 1 \ \ \ \ \ (6)$

of (5), which looks within reach of current methods (and was even claimed without proof by Erdos), but does not have a full proof in the literature at present.

In the final section of the paper we discuss some near counterexamples to the strong conjecture (1) that indicate that it is likely going to be difficult to get close to proving this conjecture without assuming some rather strong hypotheses. Firstly, we show that failure of Legendre’s conjecture on the existence of a prime between any two consecutive squares can lead to a counterexample to (1). Secondly, we show that failure of the Dickson-Hardy-Littlewood conjecture can lead to a separate (and more dramatic) failure of (1), in which the primes are no longer the dominant sequence on which the totient function is non-decreasing, but rather the numbers which are a power of two times a prime become the dominant sequence. This suggests that any significant improvement to (2) would require assuming something comparable to the prime tuples conjecture, and perhaps also some unproven hypotheses on prime gaps.