Dror Bar-Natan and Roland Van der Veen – A Fast, Strong, and Fun knot invariant!

Combinatorics and more 2025-09-25

Dror Bar-Natan (homepage, Wikipedia) told me about his work with Roland Van der Veen (homepage, arXiv, YouTube) on a wonderful knot invariant which distinguishes knots much better than other knot invariants, and can be computed quickly even for knots of hundreds of crossings. (I already mentioned it here.) Let me devote this post to this cheerful breakthrough.

Shana Tova (happy new Jewish year) to all our readers from the beautiful city of Boise, Idaho. I repeat my prayers and wishes from last year for an end of the terrible war and for peace.

Other recent news on knots: As most of you probably heard, Mark Brittenham and Susan Hermiller recently disproved a longstanding conjecture and showed that Unknotting number is not additive under connected sum. Their work is featured in an article by Leila Sloman in Quanta Magazine.

Videotaped lectures

Here are three videotaped lectures by Dror about the invariants: Easy: https://www.math.toronto.edu/~drorbn/Talks/Toronto-241030/index.html;

Dreamy: https://www.math.toronto.edu/~drorbn/Talks/Pitzer-250308/index.html; and

Tougher: https://www.math.toronto.edu/~drorbn/Talks/Bonn-2505/index.html.

A nice quote: “If those look to you similar to Feynman’s diagrams it is because they are Feynman’s diagrams”.

Dror Bar-Natan and Roland Van der Veen, A fast, strong, topologically meaningful, and fun knot invariant

Abstract: In this paper we discuss a pair of polynomial knot invariants $\Theta = (\Delta,\phi)$ which is:

Theoretically and practically fast: Θ can be computed in polynomial time. We can compute it in full on random knots with over 300 crossings, and its evaluation at simple rational numbers on random knots with over 600 crossings.‚
Strong: Its separation power is much greater than the hyperbolic volume, the HOMFLY-PT polynomial and Khovanov homology (taken together) on knots with up to 15 crossings (while being computable on much larger knots).
Topologically meaningful: It likely gives a genus bound, and there are reasons to hope that it would do more.
Fun: Scroll to Figures 1.1–1.4 and 3.1.

∆ is merely the Alexander polynomial. θ is almost certainly equal to an invariant that was studied extensively by Ohtsuki [Oh2], continuing Rozansky, Kricker, and Garoufalidis [Roz1, Roz2, Roz3, Kr, GR]. Yet our formulas, proofs, and programs are much simpler and enable its computation even on very large knots.

Graphic description

The Alexander polynomial $\Delta$ is represented by a “bar code” representing the signs of the coefficients. The invariant $\theta$ is described by a two-dimensional array of colors (an “hexagonal QR code”) in a similar way. Below are the graphic description for three famous knots two of which are notoriously hard to distinguish.

Some more comments:

Being fast. Perhaps the most remarkable property of the invariants and the formulas by Dror and Roland is that they are practically fast. While for many invariants the limit of computation is few dozens crossings the formulas for $\Theta$ enable computations for hundreds of crossings. All these computations are also polynomial-time.
Being strong. $\Theta$ is considerably more powerful in distinguishing knots with few crossings compared to other knot invariants.
Lie algebra origins. The $\theta$ invariant was motivated from a certain $sl_3$ -based knot invariant and related calculation. This connection and its interpretation is not completely clear. On the one hand, it suggests further invariants that are also computationally fast (in theory and in practice) for other Lie algebras, and on the other hand the authors believe that there should be also different foundations for $\theta$ (and perhaps further invariants of the same type) altogether.
Topological meaningfulness. Dror and Roland showed that their formulas respect Reidemeister moves so they are topological invariants. That there are further claims and hopes for connections with more natural/basic topological properties of knots like the genus, with fibered knots and with ribbon knots. As a combinatorialist, I would be quite interested in seeing invariants of knot-diagrams which are not even topologically invariant.
Being fun. There are various profound reasons why many ingredients in the work and in the lectures are fun and cheerful, especially on a gloomy background.

Pictures and a table

Dror and Roland’s paper explains the new invariants in terms of traffic rules (with curious probability flavor).

This table shows the strength of 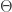$\Theta$ . For example, for the 313,230 different knots with at most 15 crossings $\Theta$ attains (313,230-6,758) distinct values.

Nostalgia Corner

Two earlier much remembered lectures by Dror.

I remember two very enlightening lectures by Dror, one from the early 90s was about finite-type (Vassiliev’s) invariants and the other, from (I think) 2001, was about Khovanov’s homology. In both lectures he gave handouts.

See this page for a more complete list of lectures by Dror since 1998.

Knots and combinatorics on this blog

Look at this post, this post, this post, this post, and this post.

Dror and I

I met Dror when he was a graduate student in Princeton (and maybe earlier) and later we were colleagues at HUJI for more than a decade. Dror and I collaborated on a single paper “Solving the Bible code puzzle” with Brendan McKay and Maya Bar-Hillel. (Here is a picture from that time of the two of us among other Bible codes skeptics.)

Dror and Roland in the Oberwolfach picture collection

Left: Dror Bar Natan (1999) right Roland Van der Veen (2011)