Instability of win probability in election forecasts (with a little bit of R)

Recently we’ve been talking a lot about election forecasting:

Election prediction markets: What happens next?

Why are we making probabilistic election forecasts? (and why don’t we put so much effort into them?)

What’s gonna happen between now and November 5?

Polling averages and political forecasts and what do you really think is gonna happen in November?

The election is coming: What forecasts should we trust?

One thing that comes up in communicating election forecasts is that people confuse probability of winning with predicted vote share. Not always—when the win probability is 90%, nobody’s thinking a candidate will get 90% of the vote—but it’s an issue in settings like the current election, where both numbers are close to 50%. If Harris is predicted to have a 60% chance of winning the electoral college, this does not imply that she’s predicted to win 60% of the electoral vote or 60% of the popular vote.

There are different ways to think about this. You could draw an S curve showing Pr(win) as a function of expected vote share. Once your expected share of the two-party vote goes below 40% or above 60%, your probability of winning becomes essentially 0 or 1. Indeed, if you get 54% of the two-party vote, this will in practice guarantee you an electoral college victory; however, an expected 54% will not translate into 100% win probability, because there’s uncertainty about the election outcome: if that forecast is 54% with a standard deviation of 2%, then there’s a chance you could actually lose.

A few years ago we did some calculations based on the assumption that the national popular vote can be forecast to within a standard deviation of 1.5 percentage point with a normally-distributed uncertainty. So if Harris is currently predicted to get 52% of the two-party vote, let’s say the forecast is that there’s a two-thirds chance she’ll get between 50.5% and 53.5% of the vote and a 95% chance she’ll get between 49% and 55% of the vote. This isn’t quite right but you could change the numbers around and get the same general picture. This forecast gives her a 90% chance of winning the popular vote (in R, the calculation is 1 – pnorm(0.5, 0.52, 0.015) = 0.91) but something like a 60% chance of winning in the electoral college—it’s only 60% and not more because the configuration of the votes in the states is such that she’ll probably need slightly more than a majority of the national vote to gain a majority of the electoral votes. As a rough calculation, we can then say she needs something like 51.6% of the two-party vote to have a 50-50 chance of winning in the electoral college (in R, the calculation is qnorm(0.4, 0.52, 0.015) = 0.516).

Now what happens if the prediction shifts? Increase Harris’s expected vote share by 0.1% (from 52% to 52.1%) and her win probability goes up by 2.5 percentage points (in R, this is pnorm(0.516, 0.52, 0.015) – pnorm(0.516, 0.521, 0.015) = 0.025).

Increase (or decrease) Harris’s expected vote share by 0.4% and her win probability goes up (or down) by 10 percentage points. The other way you can change her win probability—bringing it toward 50%—is to increase the uncertainty in your forecast.

So one reason I don’t believe in reporting win probabilities to high precision is that these win probabilities in a close election are highly sensitive to small changes in the inputs. These small changes can be important—in a close election, a 0.4% vote swing could be decisive—but that’s kind of the point: it’s the very fact that it would be likely to be decisive which makes the win probability strongly dependent on it.

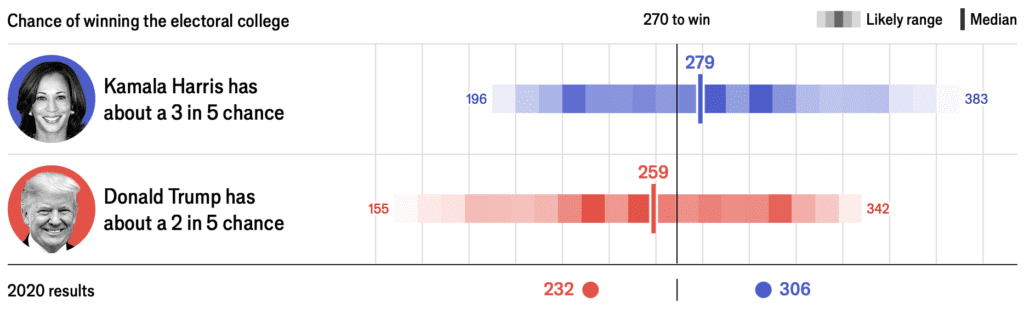
One thing I like about the Economist’s display (see image at the top of this post) is that they report the probability as “3 in 5.” This is good because it’s rounded—it’s 60%, not 58.3% or whatever. Also, I like that they say “3 in 5” rather than “60%,” because it seems less likely that this would be confused with a predicted vote share.

P.S. This is all relevant to Jessica’s recent post, partly because we coauthored a paper a few years ago (with Chris Wlezien and Elliott Morris) on information, incentives, and goals in election forecasts, and more specifically because binary predictions are hard to empirically evaluate (see here) so this is a real-world example of the common scientific problem of having to make a choice that can’t be evaluated on a purely empirical or statistical basis.